
����Ŀ����ƽ��ֱ������ϵxOy�У���M�� ![]() ��
�� ![]() �����Ե�MΪԲ�ģ�OM��Ϊ�뾶����M��ʹ��M��ֱ��OM����һ����Ϊ��B����x�ᣬy�����һ����ֱ�Ϊ��D��A����ͼ��������AM����P��
�����Ե�MΪԲ�ģ�OM��Ϊ�뾶����M��ʹ��M��ֱ��OM����һ����Ϊ��B����x�ᣬy�����һ����ֱ�Ϊ��D��A����ͼ��������AM����P�� ![]() �ϵĶ��㣮
�ϵĶ��㣮 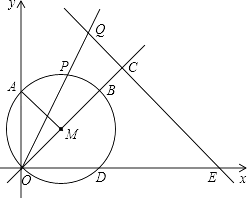
��1��д����AMB�Ķ�����
��2����Q������OP�ϣ���OPOQ=20������Q��QC��ֱ��ֱ��OM������ΪC��ֱ��QC��x���ڵ�E�� �ٵ�����P���B�غ�ʱ�����E�����ꣻ
������QD�����Q��������Ϊt����QOD�����ΪS����S��t�ĺ�����ϵʽ��S��ȡֵ��Χ��
���𰸡�
��1���⣺����M��MH��OD�ڵ�H��
�ߵ�M�� ![]() ��
�� ![]() ����
����
��OH=MH= ![]() ��
��
���MOD=45�㣬
�ߡ�AOD=90�㣬
���AOM=45�㣬
��OM=AM��
���OAM=��AOM=45�㣬
���AMO=90�㣬
���AMB=90�㣻
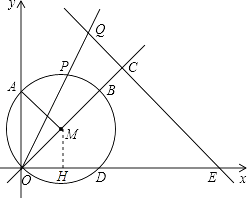
��2���⣺�١�OH=MH= ![]() ��MH��OD��
��MH��OD��
��OM= ![]() =2��OD=2OH=2
=2��OD=2OH=2 ![]() ��
��
��OB=4��
�߶���P���B�غ�ʱ��OPOQ=20��
��OQ=5��
�ߡ�OQE=90�㣬��POE=45�㣬
��OE=5 ![]() ��
��
��E��������5 ![]() ��0��
��0��
�ڡ�OD=2 ![]() ��Q��������Ϊt��
��Q��������Ϊt��
��S= ![]() ��
��
��ͼ2��������P��B���غ�ʱ������Q��QF��x�ᣬ����ΪF�㣬
��OP=4��OPOQ=20��
��OQ=5��
�ߡ�OFC=90�㣬��QOD=45�㣬
��t=QF= ![]() ��
��
��ʱS= ![]() ��
��
��ͼ3��������P��A���غ�ʱ��Q����y���ϣ�
��OP=2 ![]() ��
��
��OPOQ=20��
��t=OQ=5 ![]() ��
��
��ʱS= ![]() ��
��
��S��ȡֵ��ΧΪ5��S��10��
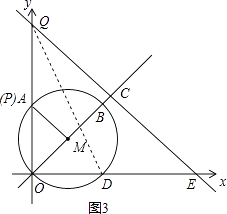

����������1�����ȹ���M��MH��OD�ڵ�H���ɵ�M�� ![]() ��
�� ![]() �����ɵá�MOH=45�㣬OH=MH=
�����ɵá�MOH=45�㣬OH=MH= ![]() ���̶���á�AOM=45�㣬����OM=AM���ɵá�AOM�ǵ���ֱ�������Σ��̶�����á�AMB�Ķ�������2������OH=MH=
���̶���á�AOM=45�㣬����OM=AM���ɵá�AOM�ǵ���ֱ�������Σ��̶�����á�AMB�Ķ�������2������OH=MH= ![]() ��MH��OD���������OD��OM��ֵ���̶��ɵ�OB�ij������ɶ���P���B�غ�ʱ��OPOQ=20�������OQ�ij����̶���ô𰸣�����OD=2
��MH��OD���������OD��OM��ֵ���̶��ɵ�OB�ij������ɶ���P���B�غ�ʱ��OPOQ=20�������OQ�ij����̶���ô𰸣�����OD=2 ![]() ��Q��������Ϊt�����ɵ�S=
��Q��������Ϊt�����ɵ�S= ![]() ��Ȼ��ֱ�ӵ�����P��B���غ�ʱ������Q��QF��x�ᣬ����ΪF�㣬�뵱����P��A���غ�ʱ��Q����y���ϣ�ȥ������⼴����ô𰸣�
��Ȼ��ֱ�ӵ�����P��B���غ�ʱ������Q��QF��x�ᣬ����ΪF�㣬�뵱����P��A���غ�ʱ��Q����y���ϣ�ȥ������⼴����ô𰸣�


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���AOBC�У���A�������ǣ���2��1������C����������4����B��C���������ֱ��ǣ� �� 
A.�� ![]() ��3��������
��3�������� ![]() ��4��
��4��
B.�� ![]() ��3��������
��3�������� ![]() ��4��??
��4��??
C.�� ![]() ��
�� ![]() ��������
�������� ![]() ��4��
��4��
D.�� ![]() ��
�� ![]() ��������
�������� ![]() ��4��
��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABC�У�ADƽ�֡�BAC������ABC�۵���ʹ��A���D�غϣ�չ�����ۺ۷ֱ�AB��AC�ڵ�E��F������DE��DF����֤���ı���AEDF�����Σ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ�ӡ���һ����ͯ�ڵĵ�����ijУѧ���μ��װ��ľ���������ȡ��У����ѧ���ľ��������ͳ�Ʒ�������Ӧ���ݵ�ͳ��ͼ���£� 
��1���������������� �� �����о��15Ԫ��ѧ�����ˣ�
��2������Уһ����500��ѧ�����ݴ��������Ƹ�Уѧ���ľ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OA=OB����PΪ��ABO�Ľ�ƽ���ߵĽ��㣬��PN��PA��x����N���ӳ�OP��AB��M��д��AO��ON��PM֮���������ϵ����֤��֮��
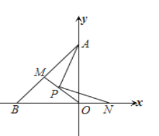
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���̽�����ýǵĶԳ��Թ���ȫ�������ν������
(1)��ͼ����OP�ǡ�MON��ƽ���ߣ��������ø�ͼ�λ�һ����OP����ֱ��Ϊ�Գ����ȫ�������Σ�(д��������������֤����������ȫ�ȣ����ó߹���ͼ��ɣ�
(2)��ͼ�ڣ�����ABC�У���ACB=90�㣬��B=60�㣬AD��CE�ֱ��ǡ�BAC����BCA��ƽ���ߣ�AD��CE�ཻ�ڵ�F.��ֱ�����:��AFE= �ȣ�DF EF(��>��<��=)��
��3����ͼ�ۣ�����ABC�У������ACB��90������(2)�е������������䣬���ʣ�����(2)�����ý����Ƿ���Ȼ����?����������֤����������������˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������20km���ס������˶���A��ȥB�أ��������г���ƽ���ٶ�Ϊ10km/h���ҳ�������ƽ���ٶ�Ϊ40km/h���ұȼ���1.5h�������������ʱ��Ϊx��h����0��x��2��
��1���������⣬��д�±���
ʱ��x��h�� ��A�صľ��� | 0.5 | 1.8 | _____ |
����A�صľ��루km�� | 5 | ���� | 20 |
����A�صľ��루km�� | 0 | 12 | ���� |
��2����ף���������A�صľ���Ϊy1��km����y2��km����д��y1��y2����x�ĺ�������ʽ��
��3����ף�������֮��ľ���Ϊy����y=12ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���kx2��4x+2=0��ʵ������
��1����k��ȡֵ��Χ��
��2������ABC�У�AB=AC=2��AB��BC�ij��Ƿ���kx2��4x+2=0����������BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC���ŵ�C˳ʱ�뷽����ת50���õ���A��B��C�䣮����A=40�㣬��B��=110�㣬���BCA��Ķ����� �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com