
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
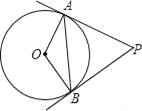
【答案】(1)、∠APB=60°;(2)、AP=![]()
【解析】试题分析:(1)、方法1,根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,可将∠APB的度数求出;方法2,证明△ABP为等边三角形,从而可将∠APB的度数求出;
(2)、方法1,作辅助线,连接OP,在Rt△OAP中,利用三角函数,可将AP的长求出;方法2,作辅助线,过点O作OD⊥AB于点D,在Rt△OAD中,将AD的长求出,从而将AB的长求出,也即AP的长.
试题解析:(1)、方法一: ∵在△ABO中,OA=OB,∠OAB=30°, ∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线, ∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°, ∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°.
方法二: ∵PA、PB是⊙O的切线∴PA=PB,OA⊥PA;
∵∠OAB=30°,OA⊥PA, ∴∠BAP=90°﹣30°=60°, ∴△ABP是等边三角形, ∴∠APB=60°.
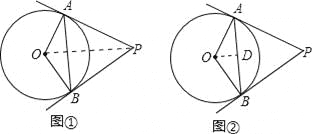
(2)、方法一:如图①,连接OP; ∵PA、PB是⊙O的切线,∴PO平分∠APB,即∠APO=![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°, ∴AP=![]() =3
=3![]() .
.
方法二:如图②,作OD⊥AB交AB于点D; ∵在△OAB中,OA=OB, ∴AD=![]() AB;
AB;
∵在Rt△AOD中,OA=3,∠OAD=30° ∴AD=OAcos30°=![]() , ∴AP=AB=3
, ∴AP=AB=3![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=![]() 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.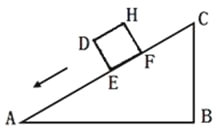
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com