Question

【题目】（1）如图①，在△ABC中，∠B=40°，∠C=80°，AD⊥BC于点D，AE平分∠BAC，求∠EAD的度数；

（2）将（1）中“∠B=40°，∠C=80°”改为“∠B=x°，∠C=y°，∠C＞∠B”，

①其他条件不变，你能用含x，y的代数式表示∠EAD吗？请写出，并说明理由；

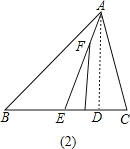
②如图②，AE平分∠BAC，F为AE上一点，FM⊥BC于点M，用含x，y的代数式表示∠EFM，并说明理由.

Answer 1

【答案】（1）∠EAD=20°；（2）①∠EAD=y-x，理由见解析；②∠EFM=y-x，理由见解析．

【解析】试题分析：（1）根据三角形内角和定理求出∠BAC，求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠EAD=∠CAE-∠CAD求出即可；

（2）根据三角形内角和定理求出∠BAC，求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠EAD=∠CAE-∠CAD求出即可；

（3）根据三角形内角和定理求出∠BAC，求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠EAD=∠CAE-∠CAD求出∠EAD，推出∠FEM=∠EAD，即可得出答案．

试题解析：（1）∵∠B=40°，∠C=80°，

∴∠BAC=180°-∠B-∠C=60°，

∵AE平分∠BAC，

∴∠CAE=∠BAC=30°，

∵AD⊥BC，

∴∠ADC=90°，

∵∠C=80°，

∴∠CAD=90°-∠C=10°，

∴∠EAD=∠CAE-∠CAD=30°-10°=20°；

（2）∵三角形的内角和等于180°，

∴∠BAC=180°-∠B-∠C=180°-x-y，

∵AE平分∠BAC，

∴∠CAE= ∠BAC= (180°xy），

∵AD⊥BC，

∴∠ADC=90°，

∴∠CAD=90°-y，

∴∠EAD=∠CAE-∠CAD= （180°-x-y）-（90°-y）=y-x；

（3）过A作AD⊥BC于D，

∵三角形的内角和等于180°，

∴∠BAC=180°-∠B-∠C，

∵AE平分∠BAC，

∴∠CAE= ∠BAC= (180°x-y），

∵AD⊥BC，

∴∠ADC=90°，

∴∠CAD=90°-y，

∴∠EAD=∠CAE-∠CAD= （180°-x-y）-（90°-y）= y-x，

∵AD⊥BC，FM⊥BC，

∴AD∥FM，

∴∠EFM=∠EAD，

∴∠EFM= y-x．