
【题目】如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
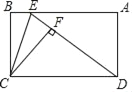
A. 6 B. 5 C. 4 D. 3
科目:初中数学 来源: 题型:
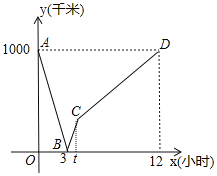
【题目】一列动车从甲地开往乙地, 一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),如图中的折线表示
(千米),如图中的折线表示![]() 与
与![]() 之间的函数关系,下列说法:①动车的速度是
之间的函数关系,下列说法:①动车的速度是![]() 千米/小时;②点B的实际意义是两车出发后
千米/小时;②点B的实际意义是两车出发后![]() 小时相遇;③甲、乙两地相距
小时相遇;③甲、乙两地相距![]() 千米;④普通列车从乙地到达甲地时间是
千米;④普通列车从乙地到达甲地时间是![]() 小时,其中不正确的有( )
小时,其中不正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
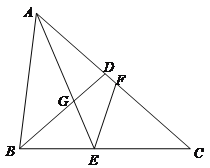
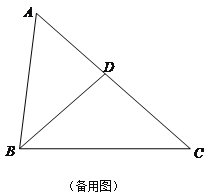
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上一点,且
,D是AC边上一点,且![]() ,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),
,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),![]() ,AE与BD相交于点G.
,AE与BD相交于点G.
(1)求证:BD平分![]() ;
;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)联结FG,当![]() 是等腰三角形时,求BE的长度.
是等腰三角形时,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
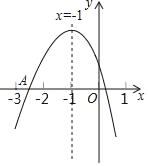
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,下列结论中:
①abc<0;②9a﹣3b+c<0;③b2﹣4ac>0;④a>b,
正确的结论是_____(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
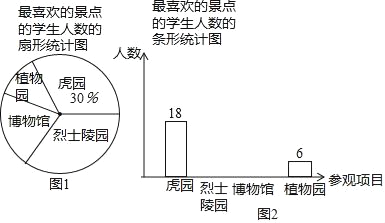
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
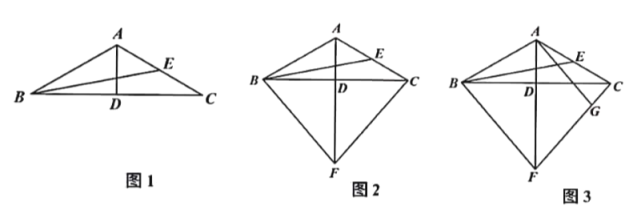
分别为![]() 的高与中线.
的高与中线.
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
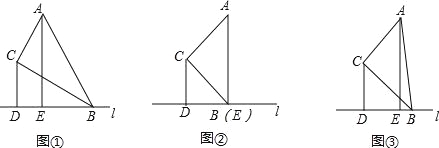
【题目】在△ABC中,∠ACB=90°经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、A做直线l的垂线,垂足分别为点D、E.
(1)问题发现:
①若∠ABC=30°,如图①,则![]() = ;
= ;
②∠ABC=45°,如图②,则![]() = ;
= ;
(2)拓展探究:
当0°<∠ABC<90°,![]() 的值有无变化?请仅就图③的情形给出证明.
的值有无变化?请仅就图③的情形给出证明.
(3)问题解决:
若直线CE、AB交于点F,![]() =
=![]() ,CD=4,请直接写出线段BD的长.
,CD=4,请直接写出线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com