
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).
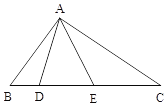
【答案】(1)45°;(2)∠DAE=30°;(3)α+2β=180.
【解析】
(1)由题意得出∠BEA=![]() ,∠CDA =
,∠CDA =![]() ,再在△ADE中
,再在△ADE中
利用内角和等于180°即可.
(2)同(1)理可快速得出答案.
(3)综合(1)(2)可总结出α与β的之间数量关系.
(1)∵AB=BE ,AC=CD
∴∠BEA=![]() ,∠CDA =
,∠CDA =![]()
在△ADE中
∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )=
(180°∠BAC )=![]() ×(180°90°)=45°
×(180°90°)=45°
(2)∠DAE=30°
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )= 30°
(180°∠BAC )= 30°
(3)α+2β=180
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )
(180°∠BAC )
∠DAE=![]() (180°∠BAC )
(180°∠BAC )
α+2β=180.


科目:初中数学 来源: 题型:
【题目】下列说法,正确的是( )
A. 若ac=bc,则a=b
B. 30.15°=30°15′
C. 一个圆被三条半径分成面积比2:3:4的三个扇形,则最小扇形的圆心角为90°
D. 钟表上的时间是9点40分,此时时针与分针所成的夹角是50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB= ![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,过对角线AC的中点O作垂线EF交边BC,AD分别为点E,F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AD=8,AB=4,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标为A(1,2),B(4,1),C(2,4).
(1)在图中画出△ABC关于y轴对称的图形△A’B’C’;
(2)在图中x轴上作出一点P,使PA+PB的值最小;并写出点P的坐标.
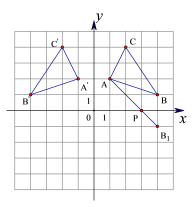
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,某市规定三口之家每月标准用水量为15立方米,单价为1.5元/立方米,超过部分单价为3元/立方米,某三口之家当月用水![]() 立方米(
立方米(![]() 且为整数)
且为整数)
⑴.请用正式表示用水![]() 立方米的费用;
立方米的费用;
⑵.三口之家当月缴水费37.50元,这月用了多少立方米的水.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快,其中正确的有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
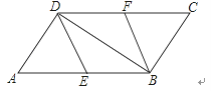
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 ![]() 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 ![]() 为直径的圆.
为直径的圆.
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
(3)某城市有四个小区 ![]() (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com