
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB= ![]() ,求⊙O半径的长.
,求⊙O半径的长.
【答案】
(1)证明:连接OD,
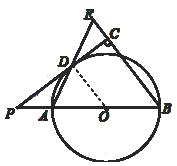
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴∠ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:由(1)知,OD∥BE,
∴∠POD=∠B,
∴cos∠POD=cosB= ![]() ,
,
在Rt△POD中,cos∠POD= ![]() ,
,
∵OD=OA,PO=PA+OA=2+OA,
∴ ![]() ,
,
∴OA=3,
∴⊙O半径等于3.
【解析】(1)连接OD,利用切线的性质和已知可证得OD∥BE,进而可得∠ADO=∠E,再由OA=OD,可得∠OAD=∠ADO,则∠OAD=∠E,根据等腰三角形的判定可证得;
(2)由OD∥BE,可得∠POD=∠B,可得cos∠POD=![]() ,在Rt△POD中,cos∠POD=
,在Rt△POD中,cos∠POD=![]() ,进而可求出OA的长,即可得半径的长.
,进而可求出OA的长,即可得半径的长.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E为AB延长线上一点,连接![]() 并延长交AD延长线于点
并延长交AD延长线于点![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() ;
;
图1
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 为
为![]() 的角平分线,
的角平分线,![]() 为
为![]() 的角平分线,过点
的角平分线,过点![]() 作
作![]() 交
交![]() 于点
于点![]() , 求证:
, 求证:![]() ;
;
图2 备用图
备用图
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)已知A=3x2+4xy,B=x2+3xy--y2,求:-A+2B.
(2)先化简,再求值:2(5a2-7ab+9b2)-3(14a2-2ab+3b2),其中a=![]() ,b=-
,b=-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元),图中折线OAB表示
(元),图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.
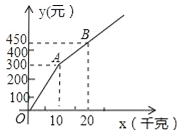
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求![]() 、
、![]() 与x的函数表达式;
与x的函数表达式;
(3)在图中画出![]() 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E,F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )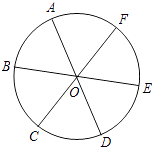
A.
B.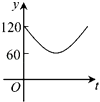
C.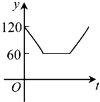
D.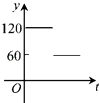
查看答案和解析>>
科目:初中数学 来源: 题型:
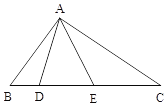
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-8mx+16m-1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2-8mx+16m-1(m>0)与线段CD有交点,请写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com