
【题目】在平面直角坐标系xOy中,抛物线y=mx2-8mx+16m-1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2-8mx+16m-1(m>0)与线段CD有交点,请写出m的取值范围.
【答案】
(1)证明:△=64m2-4m(16m-1)
=4m,
∵m>0,
∴△>0,
∴抛物线总与x轴有两个不同的交点
(2)解:根据题意,x1、x2为方程mx2-8mx+16m-1=0的两根,
∴x1+x2=- ![]() =8,x1x2=
=8,x1x2= ![]() ,
,
∵|x1-x2|=2,
∴(x1+x2)2-4x1x2=4,
∴82-4 ![]() =4,
=4,
∴m=1,
∴抛物线的解析式为y=x2-8x+15
(3)解:抛物线的对称轴为直线x=- ![]() =4,
=4,
∵抛物线开口向上,
∴当x=2,y≥0时,抛物线与线段CD有交点,
∴4m-16m+16m-1≥0,
∴m≥ ![]()
【解析】(1)证抛物线与x轴交点个数可转化为计算判别式,判断判别式的正负来判定交点个数;(2)AB可转化为两根之差,再利用根与系数关系求解;(3)要使抛物线与线段CD有交点,需x=2,y≥0,构建不等式4m-16m+16m-1≥0,可求出范围.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB= ![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快,其中正确的有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
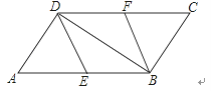
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1 , y2 , 都有点(x,y1)、(x,y2)关于点(x,x)对称,则称这两个函数为关于y=x的对称函数.例如, ![]() 和
和 ![]() 为关于y=x的对称函数.
为关于y=x的对称函数.
(1)判断:① ![]() 和
和 ![]() ;②
;② ![]() 和
和 ![]() ;③
;③ ![]() 和
和 ![]() ,其中为关于y=x的对称函数的是(填序号).
,其中为关于y=x的对称函数的是(填序号).
(2)若 ![]() 和
和 ![]() (
( ![]() )为关于y=x的对称函数.
)为关于y=x的对称函数.
①求k、b的值.
②对于任意的实数x,满足x>m时, ![]() 恒成立,则m满足的条件为 .
恒成立,则m满足的条件为 .
(3)若 ![]()
![]() 和
和 ![]() 为关于y=x的对称函数,且对于任意的实数x,都有
为关于y=x的对称函数,且对于任意的实数x,都有 ![]() ,请结合函数的图象,求n的取值范围.
,请结合函数的图象,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象上有一组点B1,B2,…,Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,则S7的值为 ,S1+S2+…+Sn= (用含n的式子表示),.
的图象上有一组点B1,B2,…,Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,则S7的值为 ,S1+S2+…+Sn= (用含n的式子表示),.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 ![]() 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 ![]() 为直径的圆.
为直径的圆.
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
(3)某城市有四个小区 ![]() (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:

(说明:成绩80分及以上为生产技能优秀,70-79分为生产技能良好,60-69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
得出结论:
a.估计乙部门生产技能优秀的员工人数为________;
b.可以推断出________部门员工的生产技能水平较高,理由为________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com