
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:

(说明:成绩80分及以上为生产技能优秀,70-79分为生产技能良好,60-69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
得出结论:
a.估计乙部门生产技能优秀的员工人数为________;
b.可以推断出________部门员工的生产技能水平较高,理由为________.(至少从两个不同的角度说明推断的合理性)
【答案】1,0,0,7,10,2;a.240;b. 甲或乙.答案不唯一,理由见解析.
【解析】
试题根据收集数据填写表格即可求解;
用乙部门优秀员工人数除以20乘以400即可得出答案,根据情况进行讨论分析,理由合理即可.
试题解析:解:填表如下:

a.![]() ×400=240(人).
×400=240(人).
故估计乙部门生产技能优秀的员工人数为 240;
b.答案不唯一,理由合理即可.
可以推断出甲部门员工的生产技能水平较高,理由为:
①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或可以推断出乙部门员工的生产技能水平较高,理由为:
①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
故答案为:1,0,0,7,10,2;
240;甲或乙,①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高;
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-8mx+16m-1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2-8mx+16m-1(m>0)与线段CD有交点,请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上对应点的位置如图所示.解答下列各题:
(1)判断下列各式的符号(填“>”或“<”)
a﹣b 0,b﹣c 0,c﹣a 0,b+c 0
(2)化简:|a﹣b|+|b﹣c|﹣|c﹣a|+|b+c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)数轴上表示5与﹣2两点之间的距离是 ,
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)如果|x﹣2|=5,则x= .
(4)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为120千米;③图中点B的坐标为(![]() ,75);④快递车从乙地返回时的速度为90千米/时.以上4个结论中正确的是( )
,75);④快递车从乙地返回时的速度为90千米/时.以上4个结论中正确的是( )
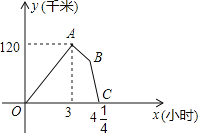
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com