
����Ŀ����֪�����������������������Ա���x��������������Ӧ�ĺ���ֵ��Ϊy1 �� y2 �� ���е㣨x��y1������x��y2�����ڵ㣨x��x���Գƣ��������������Ϊ����y=x�ĶԳƺ��������磬 ![]() ��
�� ![]() Ϊ����y=x�ĶԳƺ�����
Ϊ����y=x�ĶԳƺ�����
��1���жϣ��� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ������Ϊ����y=x�ĶԳƺ�������������ţ���
������Ϊ����y=x�ĶԳƺ�������������ţ���
��2���� ![]() ��
�� ![]() ��
�� ![]() ��Ϊ����y=x�ĶԳƺ�����
��Ϊ����y=x�ĶԳƺ�����
����k��b��ֵ��
�ڶ��������ʵ��x������x>mʱ�� ![]() ���������m���������Ϊ ��
���������m���������Ϊ ��
��3���� ![]()
![]() ��
�� ![]() Ϊ����y=x�ĶԳƺ������Ҷ��������ʵ��x������
Ϊ����y=x�ĶԳƺ������Ҷ��������ʵ��x������ ![]() �����Ϻ�����ͼ����n��ȡֵ��Χ��
�����Ϻ�����ͼ����n��ȡֵ��Χ��
���𰸡�
��1���٢�
��2����: ��y1=3x+2��y2=kx+b��k��0��Ϊ����y=x�ĶԳƺ���,��![]() =x������,�ã�3+k��x+��2+b��=2x��3+k=2,2+b=0�����k=-1,b=-2����x��mʱ,y1��y2�����,��3x+2��-x-2�����x��-1,m��-1
=x������,�ã�3+k��x+��2+b��=2x��3+k=2,2+b=0�����k=-1,b=-2����x��mʱ,y1��y2�����,��3x+2��-x-2�����x��-1,m��-1
��3���� ��y1=ax2+bx+c��a��0����y2=x2+nΪ����y=x�ĶԳƺ�������
![]() =x��
=x��
���a=-1��b=2��c=-n��
���������ʵ��x������y1��y2����
x2+n��-x2+2x-n��
����
x2+n��x��
��x2-x+n��0��
��=��-1��2-4n��0��
���n�� ![]()
����������:��1����y1=3x��y2=-x�� ![]() =
= ![]() =x��y1=3x��y2=-x����y=x�Գƺ�����
=x��y1=3x��y2=-x����y=x�Գƺ�����
��y1=x+1��y2=x-1�� ![]() =
= ![]() =x��y1=x+1��y2=x-1����y=x�Գƣ�
=x��y1=x+1��y2=x-1����y=x�Գƣ�
��y1=x2+1��y2=x2-1�� ![]() =
= ![]() =x2��x��y1=x2+1��y2=x2-1������y=x�Գƣ�
=x2��x��y1=x2+1��y2=x2-1������y=x�Գƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������Ҳ�ݮ��ժ�IJ�ݮƷ����ͬ�����ۼ۸�Ҳ��ͬ������һ�ڼ䡱�����Ҿ��Ƴ����Żݷ������ײ�ժ���Żݷ����ǣ��οͽ��蹺��50Ԫ����Ʊ����ժ�IJ�ݮ�����Żݣ��Ҳ�ժ���Żݷ����ǣ��οͽ����蹺����Ʊ����ժ�IJ�ݮ����һ�������������ִ����Żݣ��Ż��ڼ䣬��ij�ο͵IJ�ݮ��ժ��Ϊx��ǧ�ˣ����ڼײ�ժ�����ܷ���Ϊ![]() ��Ԫ�������Ҳ�ժ�����ܷ���Ϊ
��Ԫ�������Ҳ�ժ�����ܷ���Ϊ![]() ��Ԫ����ͼ������OAB��ʾ
��Ԫ����ͼ������OAB��ʾ![]() ��x֮��ĺ�����ϵ��
��x֮��ĺ�����ϵ��
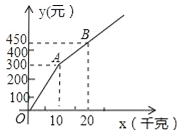
��1���ס�������ժ�Ż�ǰ�IJ�ݮ���ۼ۸���ÿǧ�� Ԫ��
��2����![]() ��
��![]() ��x�ĺ�������ʽ��
��x�ĺ�������ʽ��
��3����ͼ�л���![]() ��x�ĺ���ͼ��д��ѡ��ײ�ժ�����ܷ��ý���ʱ����ݮ��ժ��x�ķ�Χ��
��x�ĺ���ͼ��д��ѡ��ײ�ժ�����ܷ��ý���ʱ����ݮ��ժ��x�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����в���ȷ����(����)

A. ��AB��BCʱ���������� B. ��AC��BDʱ����������
C. ����ABC��90��ʱ�����Ǿ��� D. ��AC��BDʱ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC �У�AB=AC����ABΪֱ���ġ�O��BC�ཻ�ڵ�D����CA���ӳ����ཻ�ڵ�E������D��DF��AC�ڵ�F��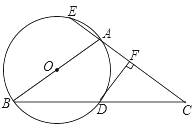
��1����֤��DF�ǡ�O�����ߣ�
��2���� ![]() ���뾶OA=3����AE�ij���
���뾶OA=3����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=mx2-8mx+16m-1��m��0����x��Ľ���ֱ�ΪA��x1 �� 0����B��x2 �� 0����
��1����֤������������x����������ͬ�Ľ��㣻
��2����AB=2����������ߵĽ���ʽ��
��3����֪x��������C��2��0����D��5��0������������y=mx2-8mx+16m-1��m��0�����߶�CD�н��㣬��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c����|a-![]() |+
|+![]() +(c-
+(c-![]() )2=0.
)2=0.
(1)��a��b��c��ֵ��
(2)������a��b��cΪ���ܷ�������?������������ܳ�������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ղ���д���ɣ�
(1)����1=��2������AD��BC__________��
(2)����A+��ABC=180��������AD��BC________��
(3)��Ϊ_____��________��������C+��ABC=180��(��ֱ��ƽ�У�ͬ���ڽǻ���)
(4)��Ϊ______��______��������3=��C(��ֱ��ƽ�У�ͬλ�����)��
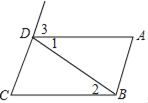
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�DZ�����һ�ֲ�Ʒ30�������ͼ��ͼ1�Dz�Ʒ��������y(��λ����)��ʱ��t(��λ����)�ĺ�����ϵ��ͼ2��һ����Ʒ����������z(��λ��Ԫ)��ʱ��t(��λ����)�ĺ�����ϵ����֪��������������������һ����Ʒ�������������н��۴������( )

A. ��24���������Ϊ200�� B. ��10������һ����Ʒ��������15Ԫ
C. ��12�����30���������������������� D. ��30���������������750Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������a��b��c�������϶�Ӧ���λ����ͼ��ʾ��������и��⣺
��1���ж����и�ʽ�ķ��ţ�������������������
a��b�� ��0��b��c�� ��0��c��a�� ��0��b+c�� ��0
��2������|a��b|+|b��c|��|c��a|+|b+c|��
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com