
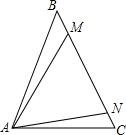
 如图,在已知△ABC中,AB=AC,MN=NA,∠BAM=∠NAC,则∠MAN=60°.
如图,在已知△ABC中,AB=AC,MN=NA,∠BAM=∠NAC,则∠MAN=60°.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
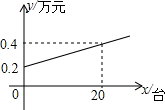 某商场负责空调销售的营销人员的工资结构是基本工资加销售提成,该商场5月份销售的甲、乙两种空调的进价和售价如表,而营销人员工资y与总销量x的函数图象如图所示:
某商场负责空调销售的营销人员的工资结构是基本工资加销售提成,该商场5月份销售的甲、乙两种空调的进价和售价如表,而营销人员工资y与总销量x的函数图象如图所示:| 甲 | 乙 | |
| 进价(万元/台) | 0.4 | 0.5 |
| 售价(万元/台) | 0.55 | 0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
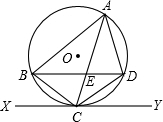 如图,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC,BD相交于点E.
如图,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC,BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com