练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    观察下列各式：

    13=12

    13+23=32

    13+23+33=62

    13+23+33+43=102

    …

    猜想13+23+33+…+103=　


    552　．

                  解：根据数据可分析出规律为从1开始，连续n个数的立方和=（1+2+…+n）2

    所以13+23+33+…+103=（1+2+3…+10）2=552．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    计算：（﹣1）（+1）﹣（﹣）﹣2+|1﹣|﹣（π﹣2）0+．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知x2﹣2x﹣3=0，则2x2﹣4x的值为（　　）

    A．  ﹣6           B．6             C．﹣2或6       D． ﹣2或30

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察下列各式你会发现什么规律？

    1×5=5，而5=32﹣22

    2×6=12，而12=42﹣22

    3×7=21，而21=52﹣22

    …

    （1）求10×14的值，并写出与题目相符合的形式；

    （2）将你猜想的规律用只含一个字母n的等式表示出来，并说明等式的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若（x﹣1）2=2，则代数式2x2﹣4x+5的值为（　　）

    A．  11            B．6             C．7             D． 8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用同样大小的黑色棋子按如图所示的规律摆放：

    （1）第5个图形有多少黑色棋子？

    （2）第几个图形有2013颗黑色棋子？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在求1+6+62+63+64+65+66+67+68+69的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：

    S=1+6+62+63+64+65+66+67+68+69①

    然后在①式的两边都乘以6，得：

    6S=6+62+63+64+65+66+67+68+69+610②

    ②﹣①得6S﹣S=610﹣1，即5S=610﹣1，所以S=，得出答案后，爱动脑筋的小林想：

    如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a2+a3+a4+…+a2014的值？你的答案是（　　）

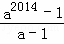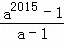    A．       B．     C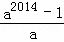．     D． a2014﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值．（a+b）（a﹣b）+b（a+2b）﹣b2，其中a=1，b=﹣2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若ab=2，a﹣b=﹣1，则代数式a2b﹣ab2的值等于　

    查看答案和解析>>

    同步练习册答案