
 经过点(
经过点( ,
, ).
). 的值;
的值; ,
, ),用含
),用含 的式子分别表示
的式子分别表示 和
和 ,并求
,并求 与
与 之间的函数关系式;
之间的函数关系式; ,且对于任意的实数
,且对于任意的实数 ,都有
,都有 ≥
≥ ,直接写出
,直接写出 的取值范围.
的取值范围.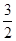 (2)q=-p2+p+
(2)q=-p2+p+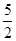 (3)-
(3)-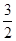 ≤m≤
≤m≤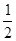 且m≠0
且m≠0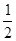 )经过抛物线,∴代入解析式得出n-m的值(2)将点(p,q)代入解析式。解:(1)∵抛物线
)经过抛物线,∴代入解析式得出n-m的值(2)将点(p,q)代入解析式。解:(1)∵抛物线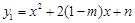 经过点(
经过点( ,
,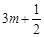 ),
),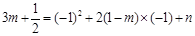 .
. 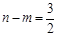 . ............................................................. 1分
. ............................................................. 1分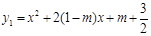 ,
,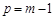 , ............................................................. 2分
, ............................................................. 2分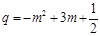 . .......................................................... 3分
. .......................................................... 3分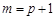 ,
,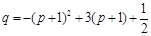 .
. . ........................................................ 5分
. ........................................................ 5分 的取值范围为
的取值范围为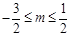 且
且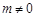 . .................................... 7分
. .................................... 7分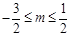 或只写
或只写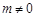 得1分.
得1分.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
 的图象中,观察得出了下面五条信息:
的图象中,观察得出了下面五条信息:
 ;②
;② ;③
;③ ;
; ;⑤
;⑤ .
. | A.①②④ | B.①③⑤ | C.②③⑤ | D.①③④⑤ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=x2-2x-1 | B.y=-x2+2x-1 |
| C.y=x2+2x-1 | D.y=-x2+4x+1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过(2,1)和(6,-5)两点.
经过(2,1)和(6,-5)两点.
 右侧的此抛物线上一点,过点P作PM
右侧的此抛物线上一点,过点P作PM
 轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标; 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

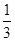 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式; ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 轴交于点
轴交于点 ,与
,与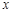 轴交于
轴交于 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线 ,与抛物线相交于点
,与抛物线相交于点 ,与对称轴交于点N,点
,与对称轴交于点N,点 为直线
为直线 上的一个动点,过P作
上的一个动点,过P作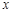 轴的垂线交抛物线于点G,设线段PG的长度为
轴的垂线交抛物线于点G,设线段PG的长度为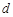

 <5时,请用含
<5时,请用含 的代数式表示
的代数式表示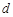 ,求出
,求出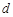 的最大值
的最大值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com