
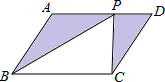
 如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 无法确定 |
分析 根据平行四边形的面积公式可得S△PBC=$\frac{1}{2}$S平行四边形ABCD,进而可得S△ABP+S△PDC═$\frac{1}{2}$S平行四边形ABCD,然后再由条件S△ABP=3,S△PDC=2,可得S平行四边形ABCD=(3+2)×2=10.
解答 解:∵P是?ABCD上一点,
∴S△PBC=$\frac{1}{2}$S平行四边形ABCD,
∴S△ABP+S△PDC═$\frac{1}{2}$S平行四边形ABCD,
∵S△ABP=3,S△PDC=2,
∴S平行四边形ABCD=(3+2)×2=10,
故选:C.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的面积公式=×高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
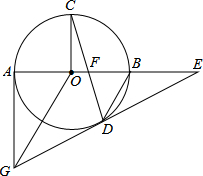 如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.
如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com