
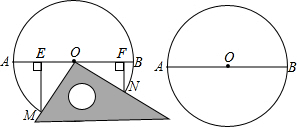
分析 (1)运用HL证明△MOE≌△NOF,得到ME=OF,NF=OE,即可证明结论;
(2)运用类比思想,分别探究当E、F在点O两侧时和当E、F在点O同侧时,三条线段的数量关系.
解答 解:(1)如图1所示,
∵三角尺的两条直角边分别与⊙O交于M、N两点;直角顶点在圆心O上,
∴OM=ON,∠MPN=90°,
∵ME⊥AB,NF⊥AB,
∴∠OEM=∠OFN=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∴△MOE≌△NOF(HL),
∴ME=OF,NF=OE,
∴EF=OE+OF=NF+ME;
(2)EF与ME、NF的数量关系发生变化
当E、F在点O两侧时,如图1所示,EF=ME+NF;
当E、F在点O同侧时,同(1)可证△MOE≌△NOF,
∴ME=OF,NF=OE,
如图2所示,当OF>OE时,EF=OF-OE=ME-NF,
如图3所示,当OE>OF时,EF=OE-OF=NF-ME.
点评 本题主要考查了三角形全等的判定与性质,运用类比思想探究E、F在不同位置三线段的数量关系如何变化.


科目:初中数学 来源: 题型:填空题
 如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.
如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
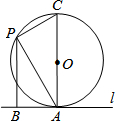 如图,直线l与半径为6的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于B点,连结AO并延长交⊙O于C点,连结PA、PC.①∠APC=90°度;②设PA=x,PB=y,则(x-y)的最大值是3.
如图,直线l与半径为6的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于B点,连结AO并延长交⊙O于C点,连结PA、PC.①∠APC=90°度;②设PA=x,PB=y,则(x-y)的最大值是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
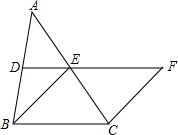 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com