
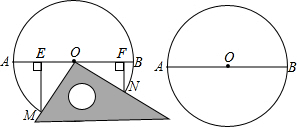
 如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.
如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.  一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
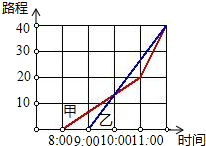 如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com