
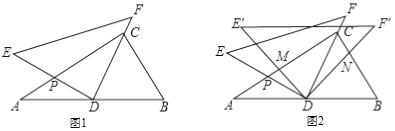
����Ŀ����һ�����dzߣ���Rt��ABC�У���ACB=90�㣬��B=60������Rt��DEF�У���EDF=90�㣬��E=45������ͼ1�ڷţ���DΪAB�ߵ��е㣬DE��AC�ڵ�P��DF������C����BC=2.
��1����֤����ADC����APD��
��2������APD�������
��3����ͼ2������DEF�Ƶ�D˳ʱ�뷽����ת������0�㣼����60��������ʱ�ĵ���ֱ�����dz�Ϊ��DE��F�䣬DE����AC�ڵ�M��DF����BC�ڵ�N�����ж�![]() ��ֵ�Ƿ��������ı仯���仯��������䣬�����
��ֵ�Ƿ��������ı仯���仯��������䣬�����![]() ��ֵ����֮����˵�����ɣ�
��ֵ����֮����˵�����ɣ�
���𰸡�(1)������;(2) ![]() ;(3) �����������ı仯���仯
;(3) �����������ı仯���仯
��������
��1�����жϳ���BCD�ǵȱ������Σ����������ADP=��ACD�����ɵó����ۣ�
��2�����PH������������ε������ʽ���ɵó����ۣ�
��3��ֻҪ֤����DPM����DCN���ƣ��ٸ������������ζ�Ӧ�߳ɱ�������֤����
��1��֤�����ߡ�ABC��ֱ�������Σ���D��AB���е㣬
��AD=BD=CD��
������BCD�У�BC=BD�ҡ�B=60����
���BCD�ǵȱ������Σ�
���BCD=��BDC=60����
���ACD=90������BCD=30����
��ADE=180������BDC����EDF=30����
����ADC����APD����A=��A����ACD=��ADP��
���ADC�ס�APD.
��2���ɣ�1���ѵ���BCD�ǵȱ������Σ���BD=BC=AD=2��
����P��PH��AD�ڵ�H��
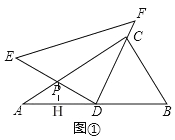
�ߡ�ADP=30��=90������B=��A��
��AH=DH=1�� tanA=![]() ��
��
��PH=![]() .
.
���APD�����=![]() AD��PH=
AD��PH=![]()
��3��![]() ��ֵ�����������ı仯���仯.
��ֵ�����������ı仯���仯.
�ߡ�MPD=��A+��ADE=30��+30��=60�������MPD=��BCD=60����
����MPD����NCD����MPD=��NCD=60������PDM=��CDN=����
���MPD�ס�NCD����![]() ��
��
�ɣ�1��֪AD=CD����![]() ��
��
�ɣ�2����֪PD=2AH����PD=![]() ��
��
��![]() ��
��
��![]() ��ֵ�����������ı仯���仯.
��ֵ�����������ı仯���仯.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ��
��
��1��![]() ��
��![]() ƽ���𣿲�˵�����ɣ�
ƽ���𣿲�˵�����ɣ�
��2��д��ͼ����![]() ��ȵĽǣ���˵�����ɣ�
��ȵĽǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
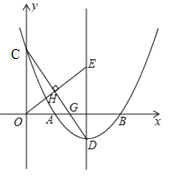
����Ŀ����ͼ��������y=![]() ��x��3��2
��x��3��2![]() ��x�ύ��A��B���㣨��A��B����ࣩ����y�ύ��C�㣬����D��
��x�ύ��A��B���㣨��A��B����ࣩ����y�ύ��C�㣬����D��
��1�����A��B��D��������ꣻ
��2������CD��x����G����ԭ��O��OE��CD������ΪH���������߶Գ�����E�����E��������ꣻ
��3���Ԣ��е�EΪԲ�ģ�1Ϊ�뾶��Բ���ڶԳ����Ҳ������������һ����P����P����E�����ߣ��е�ΪQ����PQ�ij���Сʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������6�֣��ס������˽���������Ϸ������������״��С��ȫ��ͬ���ƣ�����ֱ��������2��3��5���������Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ�
��1���״��������ȡһ���ƣ���¼���ֺ�Ż�ϴ�ȣ����������ȡһ�ţ������б�������״ͼ�ķ����������˳�ȡ��ͬ���ֵĸ��ʣ�
��2�������˳�ȡ�����ֺ�Ϊ2�ı��������ʤ������ȡ�����ֺ�Ϊ5�ı��������һ�ʤ�������Ϸ��ƽ�����ø��ʵ�֪ʶ���Խ��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��D������ֱ��ǣ�1��7������1��1������4��1������6��1������C��D��EΪ���������������ABC���ƣ����E�����겻������
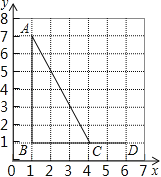
A����6��0�� B����6��3�� C����6��5�� D����4��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
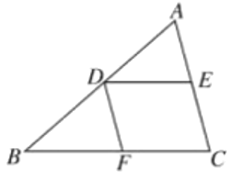
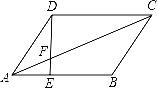
����Ŀ����֪��ͼ��ƽ���ı���ABCD�У�AE��EB=1��2��
��1����AE��DC��ֵ��
��2����AEF����CDF�����������ƣ���˵�����ɣ���������Ʊȣ�
��3�����S��AEF=6cm2����S��CDF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У���CDΪ�����ȱ�������CDE�����AED�Ķ�������������Ӧ��ͼ�β����
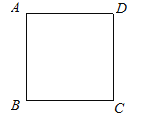
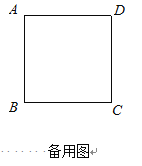
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=CB����ABC=90����DΪAB�ӳ�����һ�㣬��E��BC���ϣ���BE=BD������AE��DE��DC

����֤����ABE�ա�CBD��
������CAE=30�������BDC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com