
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.

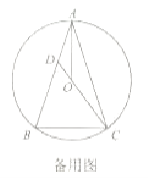
(1)求证![]() 平分
平分![]() ;
;
(2)若![]() ,求
,求![]() 和
和![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;
;![]() .
.
【解析】
试题分析:(1)连接OB,证明ΔAOB≌ΔAOC即可得出结论;
(2)过点C作CE⊥AB于E,由sin∠BAC=![]() ,设AC=5m,CE=3则可表示出AE=4m,BE=m,在RtΔCBE中,由勾股定理可求出m的值,即可得出AC的值;延长AO交BC于点H,则AH⊥BC,过点O作OF⊥AH,可求OF的值,由OF∥BC可得结论.
,设AC=5m,CE=3则可表示出AE=4m,BE=m,在RtΔCBE中,由勾股定理可求出m的值,即可得出AC的值;延长AO交BC于点H,则AH⊥BC,过点O作OF⊥AH,可求OF的值,由OF∥BC可得结论.
试题解析:(1)证明:连接OB
∵AO=AO,BO=CO,AB=AC
∴ΔAOB≌ΔAOC
∴∠BAO=∠CAO
即AO平分∠BAC
(2)过点C作CE⊥AB于E
∵sin∠BAC=![]() ,设AC=5m,则CE=3m
,设AC=5m,则CE=3m
∴AE=4m,BE=m
在RtΔCBE中,m2+(3m)2=36
∴m=![]() ,
,
∴AC=![]()
延长AO交BC于点H,则AH⊥BC,且BH=CH=3,
过点O作OF⊥AH交AB于点F,

∵∠HOC=∠BAC
∴OH=4,OC=5
∴AH=9
∴tan∠BAH=![]()
∴OF=![]() AO=
AO=![]()
∵OF∥BC
∴![]() ,即
,即
∴DC=![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源.风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在![]() 处测得塔杆顶端
处测得塔杆顶端![]() 的仰角是
的仰角是![]() ,沿
,沿![]() 方向水平前进43米到达山底
方向水平前进43米到达山底![]() 处,在山顶
处,在山顶![]() 处发现正好一叶片到达最高位置,此时测得叶片的顶端
处发现正好一叶片到达最高位置,此时测得叶片的顶端![]() (
(![]() 、
、![]() 、
、![]() 在同一直线上)的仰角是
在同一直线上)的仰角是![]() .已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高
.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高![]() 为10米,
为10米,![]() ,
,![]() ,求塔杆
,求塔杆![]() 的高.(参考数据:
的高.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠A=90°,BC的垂直平分线DE交BC于点E,交AC于点D.
(1)若∠C=35°,求∠DBA的度数;
(2)若△ABD的周长为30,AC=18,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直接坐标系![]() 中,将一块含义
中,将一块含义![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此点
恰好落在该双曲线上时停止运动,则此点![]() 的对应点
的对应点![]() 的坐标为()
的坐标为()

A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com