
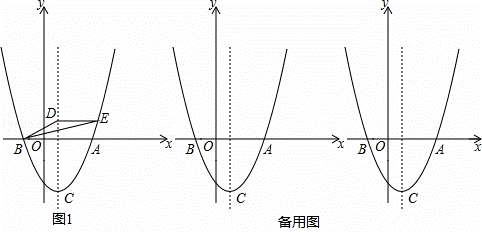
如图,已知二次函数y=x2+bx+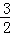 b的图象与x轴交于A、B两点(B在A的左侧),顶点为C,点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
b的图象与x轴交于A、B两点(B在A的左侧),顶点为C,点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
(1)求此二次函数的解析式和点C的坐标;
(2)当点D的坐标为(1,1)时,连接BD、BE.求证:BE平分∠ABD.
解:(1)∵点D(1,m)在y=x2+bx+ b图象的对称轴上,
b图象的对称轴上,
∴﹣ =1.
=1.
∴b=﹣2.
∴二次函数的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴C(1,﹣4).
(2)∵D(1,1),且DE垂直于y轴,
∴点E的纵坐标为1,DE平行于x轴.
∴∠DEB=∠EBO.
令y=1,则x2﹣2x﹣3=1,解得x1=1+ ,x2=1﹣
,x2=1﹣ .
.
∵点E位于对称轴右侧,
∴E(1+ ,1).
,1).
∴DE= .
.
令y=0,则x2﹣2x﹣3=0,解得x=3或﹣1,
∴点A的坐标为(3,0),点B的坐标为(﹣1,0).
∴BD=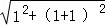 =
= .
.
∴BD=DE.
∴∠DEB=∠DBE.
∴∠DBE=∠EBO.
∴BE平分∠ABD.


科目:初中数学 来源: 题型:
二次函数y=﹣x2+(3+k)x+2k﹣1的图象与y轴的交点位于(0,5)上方,则k的范围是( )
A. k=3 B. k<3 C. k>3 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
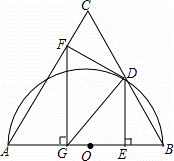
如图,已知等边△ABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.
(1)求证:DF⊥AC;
(2)若AB=8,求tan∠FGD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=﹣3x+204
(1)写出商场卖这种服装每天的销售利润y(元)与每件的销售价x(元)之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com