
分析 (1)设每件甲种学习用具的进价是a元,每件乙种学习用具的进价是b元,根据花费钱数=单价×数量,结合两种不同购进方式可列出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)结合优惠政策对x进行分段考虑,由花费钱数=单价×数量,可得出y关于x的函数关系式;
(3)找出购进乙种学习用具x件的花费,令乙种的花费<甲种的花费找出关于x的一元一次不等式,解出不等式即可得出结论.
解答 解(1)设每件甲种学习用具的进价是a元,每件乙种学习用具的进价是b元,
根据题意得:$\left\{\begin{array}{l}{5a+3b=231}\\{2a+3b=141}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=30}\\{b=27}\end{array}\right.$.
答:每件甲种学习用具的进价是30元,每件乙种学习用具的进价是27元.
(2)当0<x≤20时,y=30x;
当x>20时,y=20×30+0.7×30(x-20)=21x+180.
(3)购买x件乙种学习用具的花费为27x元,购买x件甲种学习用具的花费为(21x+180)元,
令27x<21x+180,解得:x<30.
即:当20<x<30时,购进乙种学习用具更省钱;当x=30时,两种学习用具的花费一样;当x>30时,购买甲种学习用具更省钱.
点评 本题考查了解二元一次方程组、一次函数的应用以及解一元一次不等式,解题的关键是:(1)根据已知列出关于a、b的二元一次方程组;(2)结合优惠政策分段寻找函数解析式;(3)令购买乙种的花费<购买甲种的花费找出此时的x的取值范围.本题属于中档题,难度不大,解决该类型题目时,把握住数量关系是关键.


科目:初中数学 来源: 题型:填空题
 如图,有一张长为8cm,宽为7cm的矩形纸片ABCD,现要剪下一个腰长为6cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm2.
如图,有一张长为8cm,宽为7cm的矩形纸片ABCD,现要剪下一个腰长为6cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
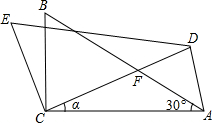 如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.
如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com