
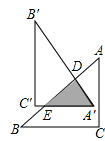
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是 .
科目:初中数学 来源: 题型:
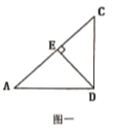
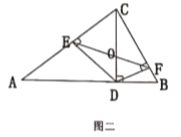
【题目】如图,在![]() 中,过点
中,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() .连接
.连接![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)在图一![]() 中,
中,![]() ,
,![]() ,有几组相似的三角形,请写出来;
,有几组相似的三角形,请写出来;
(2)在图二中,证明:![]() ;
;
(3)如果![]() ,
,![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连拉
,连拉![]() .
.
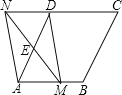
(1)求证:四边形![]() 是平行四边形。
是平行四边形。
(2)填空:
①当![]() 的值为_______________时,四边形
的值为_______________时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为_______________时,四边形
的值为_______________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“元旦”联欢晚会,其中有一个转转盘抽奖环节,有两名幸运观众分别转动如图所示的转盘各一次(转盘被分成四个相等的扇形区域,分别写有“兔子玩偶”、“熊猫玩偶”、“猴子玩偶”、“才艺表演”),转盘停止后(指针指在分界线时重转),若指针指向某种玩偶,则获得相应的玩偶,若指针指向才艺表演,则要在舞台上进行才艺表演且没有任何奖品,小娟和小寒是这两名幸运观众,用树状图或列表的方法求小娟和小寒均要进行才艺表演的概率.
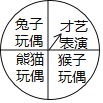
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点P从点A开始沿边AB向B以
,动点P从点A开始沿边AB向B以![]() 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以
的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以![]() 的速度移动(不与点C重合),如果P、Q分别从A、B同时出发,设运动的时间为
的速度移动(不与点C重合),如果P、Q分别从A、B同时出发,设运动的时间为![]() ,四边形APQC的面积为
,四边形APQC的面积为![]() .
.
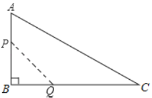
(1)求y与x之间的函数关系式;写出自变量x的取值范围;
(2)当四边形APQC的面积等于![]() 时,求x的值;
时,求x的值;
(3)四边形APQC的面积能否等于![]() ?若能,求出运动的时间,若不能,说明理由.
?若能,求出运动的时间,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(3,0),其部分图象如图所示,下列结论:
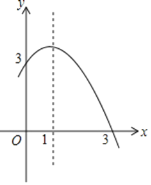
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=-2 x2=3;
③3a+c=0;
④当y>0时,x的取值范围是-1<x<3;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+2的图象与y轴交于点C,与反比例函数y2=![]() 的图象交于A、B两点,点B的横坐标为﹣2,S△AOC=1,tan=∠AOC=
的图象交于A、B两点,点B的横坐标为﹣2,S△AOC=1,tan=∠AOC=![]() .
.
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出kx+2﹣![]() >0时自变量x的取值范围.
>0时自变量x的取值范围.
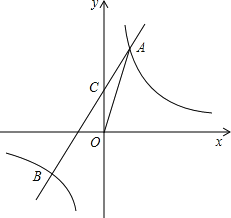
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com