
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Ε·ΒψP¥”ΒψAΩΣ Φ―Ί±ΏABœρB“‘
Θ§Ε·ΒψP¥”ΒψAΩΣ Φ―Ί±ΏABœρB“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ®≤Μ”κΒψB÷ΊΚœΘ©Θ§Ε·ΒψQ¥”ΒψBΩΣ Φ―Ί±ΏBCœρC“‘
ΒΡΥΌΕ»“ΤΕ·Θ®≤Μ”κΒψB÷ΊΚœΘ©Θ§Ε·ΒψQ¥”ΒψBΩΣ Φ―Ί±ΏBCœρC“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ®≤Μ”κΒψC÷ΊΚœΘ©Θ§»γΙϊPΓΔQΖ÷±π¥”AΓΔBΆ§ ±≥ωΖΔΘ§…η‘ΥΕ·ΒΡ ±ΦδΈΣ
ΒΡΥΌΕ»“ΤΕ·Θ®≤Μ”κΒψC÷ΊΚœΘ©Θ§»γΙϊPΓΔQΖ÷±π¥”AΓΔBΆ§ ±≥ωΖΔΘ§…η‘ΥΕ·ΒΡ ±ΦδΈΣ![]() Θ§ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΈΣ
Θ§ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΈΣ![]() Θ°
Θ°
Θ®1Θ©«σy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ–¥≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©Β±ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΒ»”Ύ![]() ±Θ§«σxΒΡ÷ΒΘΜ
±Θ§«σxΒΡ÷ΒΘΜ
Θ®3Θ©ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΡήΖώΒ»”Ύ![]() ΘΩ»τΡήΘ§«σ≥ω‘ΥΕ·ΒΡ ±ΦδΘ§»τ≤ΜΡήΘ§ΥΒΟςάμ”…Θ°
ΘΩ»τΡήΘ§«σ≥ω‘ΥΕ·ΒΡ ±ΦδΘ§»τ≤ΜΡήΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ°
Θ°![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ§
Θ§![]() ΘΜΘ®3Θ©≤ΜΡήΘ§άμ”…ΦϊΫβΈω.
ΘΜΘ®3Θ©≤ΜΡήΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”ΟΝΫΗω÷±Ϋ«»ΐΫ«–ΈΒΡΟφΜΐ≤ν«σΒΟ¥πΑΗΦ¥Ω…ΘΜ
Θ®2Θ©‘ΎΚ· ΐΫβΈω Ϋ÷–Θ§Ννy=112Θ§ΫβΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®3Θ©‘ΎΚ· ΐΫβΈω Ϋ÷–Θ§Ννy=172Θ§ΫβΖΫ≥ΧΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΓΏ≥ωΖΔ ±ΦδΈΣxΘ§ΒψPΒΡΥΌΕ»ΈΣ![]() Θ§ΒψQΒΡΥΌΕ»ΈΣ
Θ§ΒψQΒΡΥΌΕ»ΈΣ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ°Γύ
Θ°Γύ![]() Θ°
Θ°![]() Θ°
Θ°
Θ®2Θ©“άΧβ“βΒΟΘΚ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§![]() Θ§
Θ§
Θ®3Θ©≤ΜΡήΘ§άμ”…ΘΚ
![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§![]() Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©
Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©
“ρΈΣ![]() Θ°Υυ“‘
Θ°Υυ“‘![]() ≤Μ‘ΎΖΕΈßΡΎΘ§Υυ“‘ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐ≤ΜΡήΒ»”Ύ
≤Μ‘ΎΖΕΈßΡΎΘ§Υυ“‘ΥΡ±Ώ–ΈAPQCΒΡΟφΜΐ≤ΜΡήΒ»”Ύ![]() Θ°
Θ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
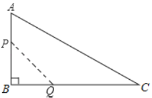
ΓΨΧβΡΩΓΩ »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΓςABC «÷±Ϋ«»ΐΫ«–ΈΘ§ΓœACB=90ΓψΘ§AC=BCΘ§OA=1Θ§OC=4Θ§≈ΉΈοœΏy=x2+bx+cΨ≠ΙΐAΘ§BΝΫΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΒψE «÷±Ϋ«ΓςABC–±±ΏAB…œ“ΜΕ·ΒψΘ®ΒψAΓΔB≥ΐΆβΘ©Θ§ΙΐΒψEΉςx÷αΒΡ¥ΙœΏΫΜ≈ΉΈοœΏ”ΎΒψFΘ§Β±œΏΕΈEFΒΡ≥ΛΕ»Ήν¥σ ±Θ§«σΒψEΓΔFΒΡΉχ±ξΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬ΘΚ‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΓςEFP «“‘EFΈΣ÷±Ϋ«±ΏΒΡ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΥυ”–ΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
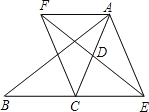
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΓςABC÷–Θ§D «ACΒΡ÷–ΒψΘ§E «œΏΕΈBC―”≥ΛœΏ…œ“ΜΒψΘ§ΙΐΒψAΉςBEΒΡΤΫ––œΏ”κœΏΕΈEDΒΡ―”≥ΛœΏΫΜ”ΎΒψFΘ§Ν§Ϋ”AEΘ§CFΘ°
Θ®1Θ©«σ÷ΛΘΚAFΘΫCEΘΜ
Θ®2Θ©»τACΘΫEFΘ§ ‘≈–ΕœΥΡ±Ώ–ΈAFCE « ≤Ο¥―υΒΡΥΡ±Ώ–ΈΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
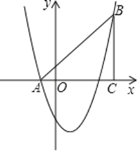
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσΫΜx÷α”ΎΒψAΘ®©¹2Θ§0Θ©ΚΆΒψBΘ§ΫΜy÷αΗΚΑκ÷α”ΎΒψCΘ§«“OBΘΫOCΘ§œ¬Ν–Ϋα¬έΘΚ
ΔΌ©¹![]() ΘΦ0ΘΜΔΎ
ΘΦ0ΘΜΔΎ![]() ΘΨ0ΘΜΔέacΘΫb©¹1ΘΜΔή4a+cΘΫ2b
ΘΨ0ΘΜΔέacΘΫb©¹1ΘΜΔή4a+cΘΫ2b
Τδ÷–’ΐ»ΖΒΡΫα¬έΗω ΐ”–Θ®ΓΓΓΓΘ©
A.1ΗωB.2ΗωC.3ΗωD.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
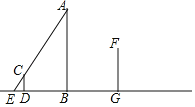
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΙΆμΘ§–ΓΜΣάϊ”Ο¬ΖΒΤA≤βΝΩΫ®÷ΰΈοGFΒΡΗΏΕ»Θ§Υϊ‘ΎΒψD¥Π ζΝΔΝΥ“ΜΗυΡΨΗΥCDΘ§≤βΒΟΡΨΗΥCDΒΡ”Α≥ΛDEΘΫ1.5mΘ§ABΓΆEGΘ§CDΓΆEGΘ§GFΓΆEGΘ°
Θ®1Θ©‘ΎΆΦ÷–Μ≠≥ω±μ ΨΫ®÷ΰΈοGF”ΑΉ”ΒΡœΏΕΈGHΘΜ
Θ®2Θ©“―÷ΣΡΨΗΥΒΡΗΏCDΘΫ2mΘ§Ϋ®÷ΰΈοGFΒΡ”ΑΉ”GHΘΫ7.8mΘ§ΡΨΗΥCD”κ¬ΖΒΤΗΥAB÷°ΦδΒΡΨύάκBDΘΫ5.85mΘ§¬ΖΒΤΗΥAB”κΫ®÷ΰΈοGF÷°ΦδΒΡΨύάκBGΘΫ6.9mΘ§«κΡψΗυΨίΧβ÷–ΧαΙ©ΒΡœύΙΊ–≈œΔΘ§«σ≥ωΫ®÷ΰΈοGFΒΡΗΏΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
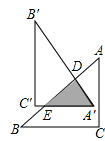
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§AC=6Θ§BC=8Θ°Α―ΓςABC»ΤAB±Ώ…œΒΡΒψDΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςAΓδBΓδCΓδΘ§AΓδCΓδΫΜAB”ΎΒψEΘ°»τAD=BEΘ§‘ρΓςAΓδDEΒΡΟφΜΐ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
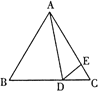
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»±ΏΓςABC÷–Θ§DΈΣBC±Ώ…œ“ΜΒψΘ§EΈΣAC±Ώ…œ“ΜΒψΘ§«“ ΓœADE=60ΓψΘ§BD=4Θ§CE=![]() Θ§‘ρΓςABCΒΡΟφΜΐ ΈΣΘ®ΓΓΓΓΘ©
Θ§‘ρΓςABCΒΡΟφΜΐ ΈΣΘ®ΓΓΓΓΘ©
A. ![]() B. 15 C.
B. 15 C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
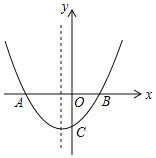
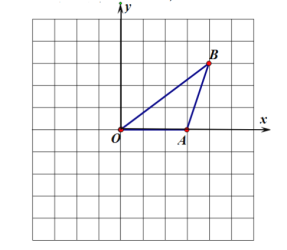
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ10ΓΝ10ΒΡΆχΗώ÷–Θ§ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΫ–ΉωΗώΒψΘ§άΐ»γAΘ®3,0Θ©Θ§BΘ®4,3Θ©ΕΦ «ΗώΒψΓΘΫΪΓςAOB»ΤΒψOΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςCODΘ®ΒψA,BΒΡΕ‘”ΠΒψΖ÷±πΈΣΒψC ΓΔDΘ©ΓΘ
Θ®1Θ©Ής≥ωΓςCODΘ§≤Δ–¥≥ωœ¬Ν–ΗςΒψΒΡΉχ±ξΘΚCΘ®ΓΓΓΓΓΓΘ©Θ§DΘ®ΓΓΓΓΓΓΘ©ΘΜ
Θ®2Θ©Ϋω”ΟΈόΩΧΕ»ΒΡ÷±≥Ώ’““ΜΗώΒψEΘ§ ΙΒΟEBΓΆABΘ§«κ±ξΟςΗώΒψEΒΡΈΜ÷ΟΘΜ
Θ®3Θ©Ϋω”ΟΈόΩΧΕ»ΒΡ÷±≥Ώ‘ΎOB…œ’““ΜΒψFΘ§ ΙΒΟΓœOAF=45Γψ(«κ±ξΟςΗ®÷ζΗώΒψMΒΡΈΜ÷Ο)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
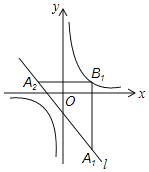
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“―÷Σ÷±œΏlΘΚyΘΫ©¹x©¹1Θ§ΥΪ«ζœΏyΘΫ![]() Θ§‘Ύl…œ»Γ“ΜΒψA1Θ§ΙΐA1Ήςx÷αΒΡ¥ΙœΏΫΜΥΪ«ζœΏ”ΎΒψB1Θ§ΙΐB1Ήςy÷αΒΡ¥ΙœΏΫΜl”ΎΒψA2Θ§«κΦΧ–χ≤ΌΉς≤ΔΧΫΨΩΘΚΙΐA2Ήςx÷αΒΡ¥ΙœΏΫΜΥΪ«ζœΏ”ΎΒψB2Θ§ΙΐB2Ήςy÷αΒΡ¥ΙœΏΫΜl”ΎΒψA3Θ§Γ≠Θ§’β―υ“ά¥ΈΒΟΒΫl…œΒΡΒψA1Θ§A2Θ§A3Θ§Γ≠Θ§AnΘ§Γ≠Φ«ΒψAnΒΡΚαΉχ±ξΈΣanΘ§»τa1ΘΫ2Θ§‘ρa2018ΘΫ_____ΘΜ»τ“ΣΫΪ…œ ω≤ΌΉςΈόœό¥ΈΒΊΫχ––œ¬»ΞΘ§‘ρa1≤ΜΩ…Ρή»ΓΒΡ÷Β «_____Θ°
Θ§‘Ύl…œ»Γ“ΜΒψA1Θ§ΙΐA1Ήςx÷αΒΡ¥ΙœΏΫΜΥΪ«ζœΏ”ΎΒψB1Θ§ΙΐB1Ήςy÷αΒΡ¥ΙœΏΫΜl”ΎΒψA2Θ§«κΦΧ–χ≤ΌΉς≤ΔΧΫΨΩΘΚΙΐA2Ήςx÷αΒΡ¥ΙœΏΫΜΥΪ«ζœΏ”ΎΒψB2Θ§ΙΐB2Ήςy÷αΒΡ¥ΙœΏΫΜl”ΎΒψA3Θ§Γ≠Θ§’β―υ“ά¥ΈΒΟΒΫl…œΒΡΒψA1Θ§A2Θ§A3Θ§Γ≠Θ§AnΘ§Γ≠Φ«ΒψAnΒΡΚαΉχ±ξΈΣanΘ§»τa1ΘΫ2Θ§‘ρa2018ΘΫ_____ΘΜ»τ“ΣΫΪ…œ ω≤ΌΉςΈόœό¥ΈΒΊΫχ––œ¬»ΞΘ§‘ρa1≤ΜΩ…Ρή»ΓΒΡ÷Β «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com