
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)对于反比例函数y=![]() ,当y<﹣1时,写出x的取值范围;
,当y<﹣1时,写出x的取值范围;
(3)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=x+1;(2)当﹣2<x<0时,y<﹣1;(3)点P的坐标为:(﹣1,﹣2).
【解析】试题分析:(1)由点A.B的横坐标分别为1,2,求得A(1,2),B(2,1),由于点A.B在一次函数y=kx+b的图象上,列方程组即可得到结论;
(2)根据图象即可得到结论;
(3)存在,根据一次函数的解析式得到D(1,0),C(0,1),设P(m,n),根据![]() 列方程即可得到结论.
列方程即可得到结论.
试题解析:(1)∵点A.B的横坐标分别为1,2,
∴y=2,或y=1,
∴A(1,2),B(2,1),
∵点A.B在一次函数y=kx+b的图象上,
∴![]()
∴![]()
∴一次函数的解析式为:y=x+1;
(2)由图象得知:y<1时,写出x的取值范围是2<x<0;
(3)存在,
对于y=x+1,当y=0时,x=1,当x=0时,y=1,
∴D(1,0),C(0,1),
设P(m,n),
![]()
![]()
∴n=2,
∵点P在反比例图象上,
∴m=1,
∴P(1,2).


科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数![]() 的图象分别交BA,BC于点D,E当AD:BD=1:3且
的图象分别交BA,BC于点D,E当AD:BD=1:3且![]() 的面积为18时,则k的值是__________________
的面积为18时,则k的值是__________________
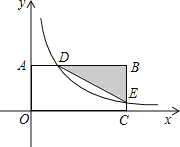
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和
(﹣2,0)之间,其部分图象如下图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第![]() 档次的产品一天的总利润为
档次的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且1≤
为正整数,且1≤![]() ≤10),求出
≤10),求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的位置如图所示,且|a|<|b|,下列各式中正确的个数是( )
①a+b<0;②b﹣a>0;③![]() ;④3a﹣b>0;⑤﹣a﹣b>0.
;④3a﹣b>0;⑤﹣a﹣b>0.
![]()
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com