
【题目】已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.
(1)当点E在正方形ABCD内部时, ①根依题意,在图1中补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG=2 ![]() ,求CE的长.(可在备用图中画图)
,求CE的长.(可在备用图中画图) 
【答案】
(1)解:当点E在正方形ABCD内部时,
①根依题意,补全图形如图1:
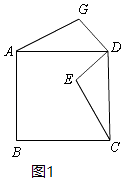
②AG=CE,AG⊥CE.
理由:
在正方形ABCD,
∴AD=CD,∠ADC=90°,
∵由DE绕着点D顺时针旋转90°得DG,
∴∠GDE=∠ADC=90°,GD=DE,
∴∠GDA=∠EDC
在△AGD和△CED中, 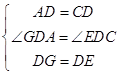 ,
,
∴△AGD≌△CED,
∴AG=CE.
延长CE分别交AG、AD于点F、H,
由①中结论△AGD≌△CED,
∴∠GAD=∠ECD,
∵∠AHF=∠CHD,
∴∠AFH=∠HDC=90°,
∴AG⊥CE.
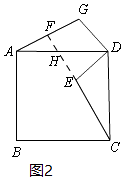
(2)解:①当点G在线段BD的延长线上时,如图3所示.
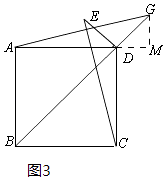
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°.
∵GM⊥AD,DG=2 ![]()
∴MD=MG=2,
∴AM=AD+DM=6
在Rt△AMG中,由勾股定理,得
AG= ![]() =2
=2 ![]() ,
,
∴CE=AG=2 ![]()
②当点G在线段BD上时,如图4所示,
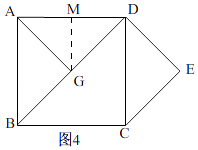
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADG=45°
∵GM⊥AD,DG=2 ![]()
∴MD=MG=2,
∴AM=AD﹣MG=2
在Rt△AMG中,由勾股定理,得
AG= ![]() =2
=2 ![]()
∴CE=AG=2 ![]()
故CE的长为2 ![]() 或2
或2 ![]() .
.
【解析】(1)①根据题意补全图形,
②先判断出∠GDA=∠EDC,进而得出△AGD≌△CED,即可得出AG=CE,最后判断出∠AFH=∠HDC=90°即可得出结论;(2)分两种情况,①当点G在线段BD的延长线上时和②当点G在线段BD上时,构造直角三角形利用勾股定理即可得出结论.
【考点精析】解答此题的关键在于理解图形的旋转的相关知识,掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列函数关系中,不能看做二次函数y=ax2+bx+c(a≠0)模型的是( )
A. 圆的半径和其面积的变化关系
B. 我国人口年自然增长率x,两年中从12亿增加到y亿的x与y的变化关系
C. 掷铅球水平距离与高度的关系
D. 面积一定的三角形底边与高的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是必然事件的是( )
A.掷一枚硬币,正面朝上B.某运动员跳高的最好成绩是20.1米
C.太阳从东方升起D.从车间刚生产的产品中任意抽取一件是次品
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都是指直线距离,图中AC⊥CB.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于点P(x,y),规定x+y=a,那么就把a叫点P的亲和数.例如:若P(2,3),则2+3=5,那么5叫P的亲和数.
(1)在平面直角坐标系中,已知,点A(﹣2,6) ①B(1,3),C(3,2),D(2,2),与点A的亲和数相等的点;
②若点E在直线y=x+6上,且与点A的亲和数相同,则点E的坐标是;
(2)如图点P是矩形GHMN边上的任意点,且点H(2,3),N(﹣2,﹣3),点Q是直线y=﹣x+b上的任意点,若存在两点P、Q的亲和数相同,那么求b的取值范围? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠XOY=90°,点A,B分别在射线OX,OY上移动.BE是
∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,则∠ACB的
大小是否变化?如果保持不变,请说明原因;如果随点A,B的移动而发生变化,求
出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
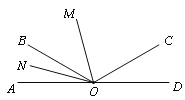
【题目】如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM、ON分别是∠AOC、∠AOB的平分线,∠MON=56°.
⑴ ∠COD与∠AOB相等吗?请说明理由;
⑵ 求∠BOC的度数;
⑶ 求∠AOB与∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com