
【题目】如图,在平面直角坐标系中,点P是以C(﹣![]() ,
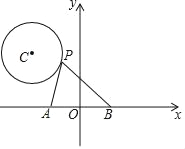
,![]() )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
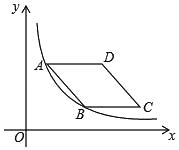
【题目】如图,菱形ABCD的边AD与x轴平行,A、B两点的横坐标分别为1和3,反比例函数y=![]() 的图象经过A、B两点,则菱形ABCD的面积是_____;
的图象经过A、B两点,则菱形ABCD的面积是_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
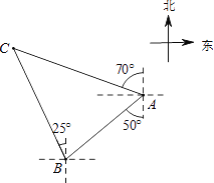
【题目】如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
(结果精确到个位,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
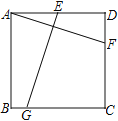
【题目】如图,在边长为6的正方形ABCD中,点F为CD上一点,E是AD的中点,且DF=2.在BC上找点G,使EG=AF,则BG的长是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
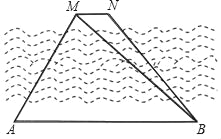
【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
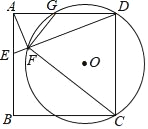
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
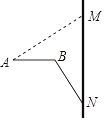
【题目】高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
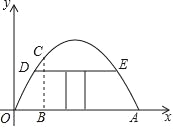
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法:①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.⑤不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0.其中说法正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com