
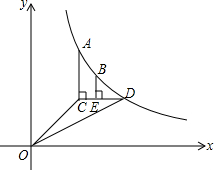
 如图,已知函数y=
如图,已知函数y=| k |
| x |
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| x |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
|
| 5 |
| 3 |
| 5 |
| 3 |
|
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
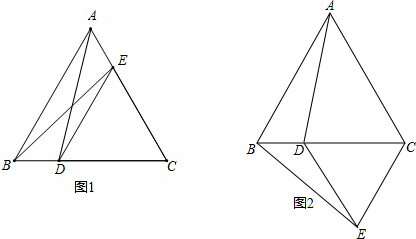
 农民王伯伯有一块地,如下图所示,已知:AB=90m,BC=120m,CD=130m,AD=140m,且∠B=90°.现在王伯伯年老力衰,要把地分给两个儿子,于是王伯伯以A、C两点划线,大儿子分得△ABC,小儿子分得△ADC.你认为王伯伯分法公平吗?请说明理由.
农民王伯伯有一块地,如下图所示,已知:AB=90m,BC=120m,CD=130m,AD=140m,且∠B=90°.现在王伯伯年老力衰,要把地分给两个儿子,于是王伯伯以A、C两点划线,大儿子分得△ABC,小儿子分得△ADC.你认为王伯伯分法公平吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
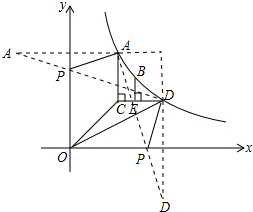
 如图,已知∠AOB=30°,P为∠AOB内一点,且OP=8.
如图,已知∠AOB=30°,P为∠AOB内一点,且OP=8.查看答案和解析>>
科目:初中数学 来源: 题型:
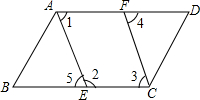 如图,根据图形完成下列填空.
如图,根据图形完成下列填空.查看答案和解析>>
科目:初中数学 来源: 题型:
 将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是
将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是查看答案和解析>>
科目:初中数学 来源: 题型:
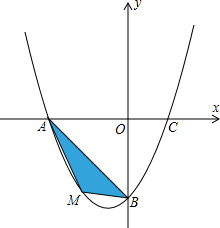 如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.
如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com