
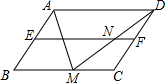
 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 过点M作MG∥AB交AD于点G,根据AD∥BC,AB∥MG可得出四边形ABMG是菱形,故可得出BM的长,再由三角形中位线定理即可得出结论.
解答 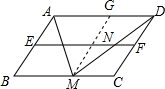 解:过点M作MG∥AB交AD于点G,
解:过点M作MG∥AB交AD于点G,
∵AD∥BC,AB∥MG,
∴四边形ABMG是平行四边形,
∴∠AGM=∠ABM.
∵AM平分∠BAD,
∴∠GAM=∠MAB,
∴∠AMB=∠AMG.
在△AGM与△ABM中,
$\left\{\begin{array}{l}∠GAM=∠BAM\\ AM=AM\\∠GAM=∠MAB\end{array}\right.$,
∴△AGM≌△ABM,
∴AB=AG=3,
∴四边形ABMG是菱形,
∴MC=5-3=2.
∵EF∥BC,点E,F分别是AB,CD的中点,
∴NF是△DCM的中位线,
∴NF=$\frac{1}{2}$MC=1.
故选B.
点评 本题考查的是三角形中位线定理,根据题意作出辅助线,构造出全等三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
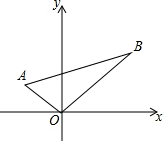 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{3}$,$\sqrt{3}$) | D. | (2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
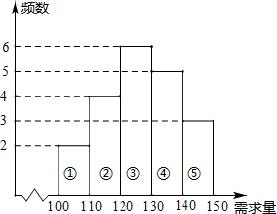 经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.
经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求:
如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+y)(y-x)=x2-y2 | B. | (x-2y)(x+2y)=x2-2y2 | ||
| C. | (2x-$\frac{1}{2}$y)2=4x2-2xy+$\frac{1}{4}$y2 | D. | (-3x-2y)2=9x2-12xy+4y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com