
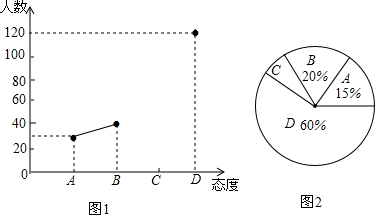
分析 (1)用D类的人数除以它所占的百分比即可得到调查的总人数;
(2)用360°乘以C类所占的百分比得到扇形C所对的圆心角的度数,再用200乘以C类所占的百分比得到C类人数,然后补全图1;
(3)画树状图展示所有12种等可能结果,再找出2人来自不同班级的结果数,然后根据概率公式求解.
解答 解:(1)120÷60%=200(人),
所以调查的家长数为200人;
(2)扇形C所对的圆心角的度数=360°×(1-20%-15%-60%)=18°,
C类的家长数=200×(1-20%-15%-60%)=10(人),
补充图为: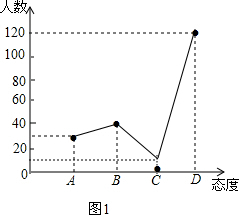
(3)设初三(1)班两名家长为A1、A2,初三(2)班两名家长为B1,B2,
画树状图为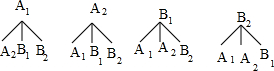
共有12种等可能结果,其中2人来自不同班级共有8种,
所以2人来自不同班级的概率=$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了扇形统计图.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
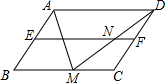 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
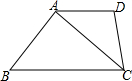 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )| A. | 9$\sqrt{7}$ | B. | 12 | C. | 8 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
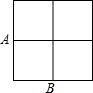 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.
如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
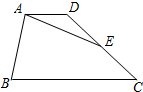 如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
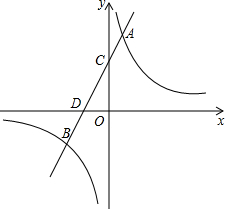 如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.
如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm~5cm之间 | B. | 5cm~6cm之间 | C. | 6cm~7cm之间 | D. | 7cm~8cm之间 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com