
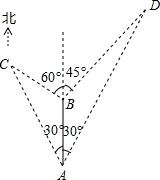
 如图,在一次数学应用活动中,小明沿一条南北公路向北行走,在A处,他测得左边建筑C在北偏西30°方向,右边建筑D在北偏东30°方向;从A出向北40米行至B处,他又测得左边建筑物C在北偏西60°方向,右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离.
如图,在一次数学应用活动中,小明沿一条南北公路向北行走,在A处,他测得左边建筑C在北偏西30°方向,右边建筑D在北偏东30°方向;从A出向北40米行至B处,他又测得左边建筑物C在北偏西60°方向,右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离.| 3 |
| 2 |
 ,
,| CE |
| tan30° |
| CE |
| tan60° |
| CE |
| tan30° |
| CE |
| tan60° |
| 3 |
| 3 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 有5张正面分别标有数字-1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后[从中任取一张,将该卡片上的数字记为m,则使关于x的二次函数y=x2-2mx+1的图象与端点为A(-1,1)和B(4,3)的线段(如图)只有一个交点的概率为
有5张正面分别标有数字-1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后[从中任取一张,将该卡片上的数字记为m,则使关于x的二次函数y=x2-2mx+1的图象与端点为A(-1,1)和B(4,3)的线段(如图)只有一个交点的概率为查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲种型号 | 乙种型号 | |
| 进价 | 3000 | 5000 |
| 售价 | 4000 | 6200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
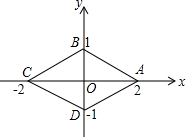 如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是
如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com