
 ��ͼ��һ�κ���y=kx+b��k��0���뷴��������y=$\frac{m}{x}$��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1��
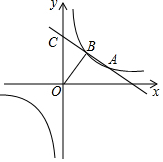
��ͼ��һ�κ���y=kx+b��k��0���뷴��������y=$\frac{m}{x}$��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1������ ��1����A��������뷴���������������m��ֵ��
��2�����B������Ϊ��n��$\frac{4}{n}$������һ�κ�������ʽ���뷴������������ʽ�У����ø���ϵ���Ĺ�ϵ���ҳ�n��k�Ĺ�ϵ���������ε������ʽ�ɱ�ʾ����b��n�Ĺ�ϵ�����ɵ�A��һ�κ���ͼ���ϣ����ҳ�k��b�Ĺ�ϵ������3����ʽΪ�����飬�ⷽ���鼴�ɵó����ۣ�
��3�����ڡ�ABD��֪����������ֱ�DZߣ����Է���������������ۣ��ֱ��ǡ�BDA=90�㣬��DBA=90�㣬��DAB=90�㣬���ݹ��ɶ����г��������ɵã�
��� �⣺��1���ѵ�A��4��1�����뷴���������еã�m=4��
�෴��������Ϊ��y=$\frac{4}{x}$��
��2���ߵ�B�ڷ���������y=$\frac{4}{x}$��ͼ���ϣ�
�����B��������n��$\frac{4}{n}$����
��y=kx+b����y=$\frac{4}{x}$�У��ã�
kx+b=$\frac{4}{x}$�������ã�kx2+bx-4=0��
��4n=-$\frac{4}{k}$����nk=-1�٣�
��y=kx+b��x=0����y=b��
����C��������0��b����
��S��BOC=$\frac{1}{2}$bn=3��
��bn=6�ڣ�
�ߵ�A��4��1����һ�κ���y=kx+b��ͼ���ϣ�
��1=4k+b�ۣ�
�����٢ڢ۳ɷ����飬��$\left\{\begin{array}{l}{nk=-1}\\{bn=6}\\{1=4k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\\{n=2}\end{array}\right.$��
���һ�κ����Ľ���ʽΪy=-$\frac{1}{2}$x+3
��3����$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=\frac{4}{x}}\end{array}\right.$�ɵ�$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$��
���B��������2��2����
��D��a��0����
��AB2=��2-4��2+��2-1��2=5��AD2=��a-4��2+��0-1��2=��a-4��2+1��BD2=��a-2��2+��0-2��2=��a-2��2+4��
����ABD=90��ʱ��AB2+BD2=AD2����5+��a-2��2+4=��a-4��2+1��
��ã�a=1������D��1��0����
����ADB=90��ʱ��AD2+BD2=AB2������a-4��2+1+��a-2��2+4=5��
�����⣬����D�����ڣ�
����BAD=90��ʱ��AB2+AD2=BD2����5+��a-4��2+1=��a-2��2+4��
��ã�a=3.5������D��3.5��0����
���ϣ���D������Ϊ��1��0����3.5��0����
���� ���⿼���˷�����������һ�κ�����������⡢�����ε������ʽ�Լ����ɶ�����֪ʶ�㣬����Ĺؼ��Ǹ��ݸ���ϵ���ҳ�����k��b��n����Ԫһ�η����飮���������е��⣬�ѶȲ���������֪ʶ��϶࣬�����������Ŀʱ���ۺ������ε������ʽ�Լ�һ�κ����ϵ�����������ó��������ǹؼ���


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{3}$ | B�� | $\frac{1}{3}$ | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5^2}=5$ | B�� | -$\sqrt{3.6}$=-0.6 | C�� | $\sqrt{{{��-13��}^2}}=-13$ | D�� | $\sqrt{36}=��6$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
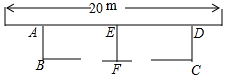 ��ͼ������һ��ǽ��ǽ�ij���Ϊ20m������34m�������Χ�������������м���һ����ʸ�����ÿ����������һ��1m�����ţ���AB�ij�Ϊx�ף�
��ͼ������һ��ǽ��ǽ�ij���Ϊ20m������34m�������Χ�������������м���һ����ʸ�����ÿ����������һ��1m�����ţ���AB�ij�Ϊx�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
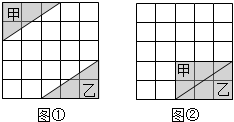 ��ͼ����5��5�ķ���ֽ�У�����ͼ�ٵ������μ�ƽ�Ƶ���ͼ����ʾ��λ�ã�����������ƴ��һ�������Σ���ȷ��ƽ�Ʒ����������Ƚ�������ƽ��3��������ƽ��2��õ���
��ͼ����5��5�ķ���ֽ�У�����ͼ�ٵ������μ�ƽ�Ƶ���ͼ����ʾ��λ�ã�����������ƴ��һ�������Σ���ȷ��ƽ�Ʒ����������Ƚ�������ƽ��3��������ƽ��2��õ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com