
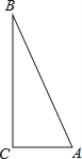
【题目】实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O;②以点O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)直线AB与⊙O的位置关系是 ;
(2)证明: ![]() ;
;
(3)若AC=5,BC=12,求⊙O的半径.
【答案】实践操作:作图见解析;
综合运用:(1)相切;(2)证明见解析;(3)⊙O的半径为![]() .
.
【解析】试题分析:(1)、根据角平分线的性质得出OC=OD,从而得出圆与直线的位置关系;(2)、根据相切的性质以及公共角得出△ABC和△OBD相似,从而得出答案;(3)、根据题意得出AD=AC=5,AB=13,则BD=8,设半径为x,则OB=12-x,根据Rt△BOD的勾股定理求出x的值,得出圆的半径.
试题解析:实践操作,如图所示:
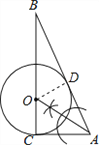
综合运用:
(1)相切
(2)因为∠BCA=90°,∠BDO=90°, 所以△ABC∽△OBD;
所以![]() 即
即![]() .
.
(3)因为AC=5,BC=12, 所以AD=5,AB=13, 所以DB=13﹣5=8,
设半径为x ,则OC=OD=x ,BO=(12﹣x), x2+82=(12﹣x)2,
解得:x=![]() .答:⊙O的半径为
.答:⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】下列事件中确定事件是( )
A.掷一枚均匀的硬币,正面朝上
B.买一注福利彩票一定会中奖
C.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球
D.掷一枚六个面分别标有,1,2,3,4,5,6的均匀正方体骰子,骰子停止转动后奇数点朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
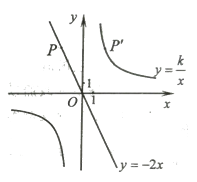
【题目】如图,已知直线y=-2x经过点P(-2,a),点P关于y轴的对称点P'在反比例函数y =![]() (k≠0)的图像上。
(k≠0)的图像上。
(1)求a的值
(2)直接写出点P'的坐标
(3)求反比例函数的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售某一种新型通讯产品.已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (万元)之间存在着如图所示的一次函数关系.
(万元)之间存在着如图所示的一次函数关系.

(1)求![]() 关于
关于![]() 的函数关系式;(直接写出结果)
的函数关系式;(直接写出结果)
(2)试写出该公司销售该种产品的月获利![]() (万元)关于销售单价
(万元)关于销售单价![]() (万元)的函数关系式.当销售单价
(万元)的函数关系式.当销售单价![]() 为何值时,月获利最大?并求这个最大值;
为何值时,月获利最大?并求这个最大值;
(月获利=月销售额-月销售产品总进价-月总开支.)
(3)若公司希望该产品一个月的销售获利不低于5万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;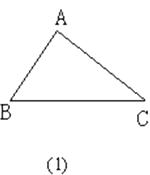
(2)如图(2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;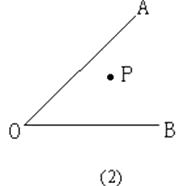
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.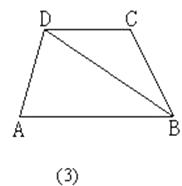
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com