【题目】如图，在△ABC中，BD⊥AC，垂足为D，AB=AC=9，BC=6，求BD的长．

参考答案：

【答案】解：作AE⊥BC于E，如图所示：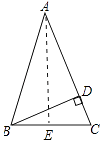
则∠AEC=90°，
∵AB=AC，
∴BE=CE= BC=3，
∴AE= =6 ，
∵BD⊥AC，
∴∠BDC=90°=∠AEC，
又∵∠C=∠C，
∴△AEC∽△BDC，
∴AE：BD=AC：BC，
∴BD= = =4 ．
【解析】作AE⊥BC于E，由等腰三角形的性质得出BE=CE= BC=3，由勾股定理求出AE，证明△AEC∽△BDC，得出对应边成比例，即可求出BD的长．
【考点精析】利用等腰三角形的性质和勾股定理的概念对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．

关闭