
【题目】我们给出如下定义:在平面直角坐标系xOy中,如果一条抛物线平移后得到的抛物线经过原抛物线的顶点,那么这条抛物线叫做原抛物线的过顶抛物线.
如下图,抛物线F2都是抛物线F1的过顶抛物线,设F1的顶点为A,F2的对称轴分别交F1、F2于点D、B,点C是点A关于直线BD的对称点.

(1)如图1,如果抛物线y=x 2的过顶抛物线为y=ax2+bx,C(2,0),那么
①a= ,b= .
②如果顺次连接A、B、C、D四点,那么四边形ABCD为( )
A.平行四边形 B.矩形 C.菱形 D.正方形
(2)如图2,抛物线y=ax2+c的过顶抛物线为F2,B(2,c-1).求四边形ABCD的面积.
(3)如果抛物线![]() 的过顶抛物线是F2,四边形ABCD的面积为
的过顶抛物线是F2,四边形ABCD的面积为![]() ,请直接写出点B的坐标.
,请直接写出点B的坐标.
【答案】(1)①a=1,b=2;②D;(2)4;(3)(![]() ,1),(
,1),(![]() ,1).
,1).
【解析】
试题分析:本题综合考查的是考生的作图能力以及二次函数的灵活运用,难度较大.
(1)已知F2的解析式,把已知坐标代入即可得出a、b的值;
(2)在(1)的基础上求出S四边形ABCD;
(3)要分情况讨论点B在点A的左边还是右边,直接写出点B的坐标即可.
试题解析:解:(1)①a=1,b=2.
②D.
(2)∵B(2,c-1),
∴AC=2×2=4.
∵当x=0,y=c,
∴A(0,c).
∵F1:y=ax2+c,B(2,c-1).
∴设F2:y=a(x-2)2+c-1.
∵点A(0,c)在F2上,
∴4a+c-1=c,
∴![]() .
.
∴BD=(4a+c)-(c-1)=2.
∴S四边形ABCD=4.
(3)(![]() ,1),(
,1),(![]() ,1).
,1).
说明:若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把8﹣(+4)+(﹣6)﹣(﹣5)写成省略加号的和的形式是( )
A.8﹣4﹣6+5
B.8﹣4﹣6﹣5
C.8+(﹣4)+(﹣6)+5
D.8+4﹣6﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
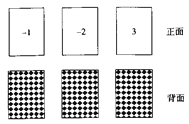
【题目】如图所示,有3张不透明的卡片,除正面写有不同的数字外,其他均相同。将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b。
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图像经过二、三、四象限的概率(用树状图或列表法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=n2﹣1,BC=2n,AC=n2+1(n为大于1的正整数),试问△ABC是直角三角形吗?若是,哪条边所对的角是直角?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 两腰对应相等的两个等腰三角形全等
B. 两锐角对应相等的两个直角三角形全等
C. 两角及其夹边对应相等的两个三角形全等
D. 面积相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值: ![]() ,其中x是不等式组
,其中x是不等式组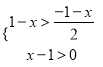 的整数解.
的整数解.
【答案】4(x﹣1),4.
【解析】试题分析:解不等式组,先求出满足不等式组的整数解.化简分式,把不等式组的整数解代入化简后的分式,求出其值.
试题解析:解不等式组,得1<x<3,
又∵x为整数,∴x=2.
原式![]()
∴原式=4×2-4=4.
【题型】解答题
【结束】
23
【题目】如图,已知A(0,4),B(-2,2),C(3,0).

(1)作△ABC关于x轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)△A1B1C1的面积S△A1B1C1=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com