
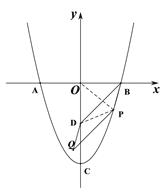
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
【答案】(1)①抛物线解析式为y=x2﹣4;②0<S四边形BDQP≤![]() ;(2)
;(2)![]() 的值与a,c无关,比值为1.
的值与a,c无关,比值为1.
【解析】试题分析:(1)①把 A(-2,0),C(0,-4)代入![]() ,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(
,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(![]() ,
, ![]() ),因A(-2,0),对称轴为
),因A(-2,0),对称轴为![]() 轴,可得B(2,0),即可得
轴,可得B(2,0),即可得![]()
![]()
![]() ,再由点P在第四象限运动,可得x单位取值范围
,再由点P在第四象限运动,可得x单位取值范围![]() ,由抛物线的图象即可得△BDP的取值范围为
,由抛物线的图象即可得△BDP的取值范围为![]() ,因
,因![]() 即可得平行四边形BDQP面积的取值范围为
即可得平行四边形BDQP面积的取值范围为![]() ;(2)过点P作PG⊥AB,设A(
;(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() ),由PG∥
),由PG∥![]() 轴,根据相似三角形的判定方法可得
轴,根据相似三角形的判定方法可得![]() ,
, ![]() ,再由相似三角形的性质可得
,再由相似三角形的性质可得![]() ,
, ![]() ,代入数值可得
,代入数值可得![]() ,
, ![]() ,把这两个式子相加可得
,把这两个式子相加可得![]() ,令
,令![]() ,即可得
,即可得![]() ,
, ![]() ,所以
,所以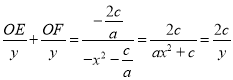 ,即
,即![]() ,所以
,所以![]() ,即可得
,即可得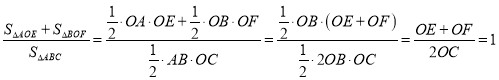
所以可得结论![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.
试题解析:
(1)①![]()
②连接DB、OP,设P(![]() ,
, ![]() )
)
∵A(-2,0),对称轴为![]() 轴
轴
∴B(2,0)
∴![]()
![]()
![]()
![]()
∵点P在第四象限运动
∴![]()
∴由抛物线的图象可得: ![]()
∵![]() ∴
∴![]()
(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() )
)

∴PG∥![]() 轴
轴
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵当![]() 时,∴
时,∴![]() ,即
,即![]() ,
, ![]()
∴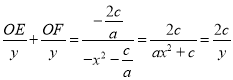
∴![]() ∴
∴![]()
∴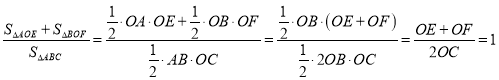
∴![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】一位“粗心”的同学在做加减运算时,将“﹣100”错写成“+100”进行运算,这样他得到的结果比正确答案( )
A.少100
B.少200
C.多100
D.多200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的塑料袋中装有红色、白色球共40个,除颜色外其它都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能 ( )
A. 4个 B. 6个 C. 34个 D. 36个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:在平面直角坐标系xOy中,如果一条抛物线平移后得到的抛物线经过原抛物线的顶点,那么这条抛物线叫做原抛物线的过顶抛物线.
如下图,抛物线F2都是抛物线F1的过顶抛物线,设F1的顶点为A,F2的对称轴分别交F1、F2于点D、B,点C是点A关于直线BD的对称点.

(1)如图1,如果抛物线y=x 2的过顶抛物线为y=ax2+bx,C(2,0),那么
①a= ,b= .
②如果顺次连接A、B、C、D四点,那么四边形ABCD为( )
A.平行四边形 B.矩形 C.菱形 D.正方形
(2)如图2,抛物线y=ax2+c的过顶抛物线为F2,B(2,c-1).求四边形ABCD的面积.
(3)如果抛物线![]() 的过顶抛物线是F2,四边形ABCD的面积为
的过顶抛物线是F2,四边形ABCD的面积为![]() ,请直接写出点B的坐标.
,请直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
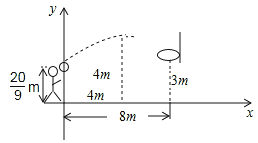
【题目】小明跳起投篮,球出手时离地面![]() m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高度4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高度4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
(1)求此抛物线对应的函数关系式;
(2)此次投篮,球能否直接命中篮筐中心?若能,请说明理由;若不能,在出手的角度和力度都不变的情况下,球出手时距离地面多少米可使球直接命中篮筐中心?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.

【答案】证明见解析.
【解析】试题分析:欲证明AB=DE,只要证明△ABC≌△DEF即可.
试题解析:∵AF=CD,
∴AC=DF,
∵BC∥EF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
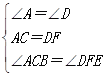 ,
,
∴△ABC≌△DEF(ASA),
∴AB=DE.
考点:全等三角形的判定与性质.
【题型】解答题
【结束】
25
【题目】如图, ![]() ,AE=BD,点D在AC边上,
,AE=BD,点D在AC边上, ![]() ,AE和BD相交于点O.
,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若![]() ,求BDE的度数.
,求BDE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com