
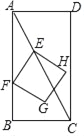
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒![]() 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
【答案】(1)点E到边AB的距离为t(2)t=1(3)S=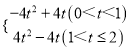 (4)当正方形EFGH的顶点与点B,D距离相等时的t值为
(4)当正方形EFGH的顶点与点B,D距离相等时的t值为![]() s或1s或
s或1s或![]() s
s
【解析】试题分析:(1)如图1中,作EM⊥AB于M.由EM∥BC,可得![]() ,即
,即![]() ,延长即可解决问题;
,延长即可解决问题;
(2)如图2中,G在AB边时,由AF+FB=4,可得2t+2t=4,解方程即可;
(3)分两种情形①如图3中,当0<t<1时,作GN⊥AB于N,EM⊥AB于M.②如图4中,当1<t≤2时,作GN⊥AB于N,EM⊥AB于M.分别求解即可;
(4)分三种情形①如图5中,当H在BD的垂直平分线上时,根据HD=HB列出方程即可解决问题;②当点E在BD的垂直平分线上时,易知AE=EC,t=1;③当点F在线段BD的垂直平分线上时,分别求解即可.
试题解析:(1)如图1中,作EM⊥AB于M.
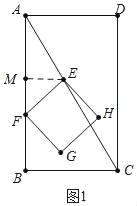
∵AB=4,BC=2,∠B=90°,
∴AC=![]() ,
,
∵EM∥BC,
∴![]() ,
,
∴![]() ,
,
∴EM=t,AM=2t.
∴点E到边AB的距离为t.
(2)如图2中,G在AB边时,
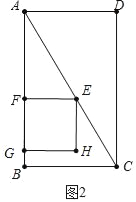
由AF+FB=4,可得2t+2t=4,
∴t=1.
(3)①如图3中,当0<t<1时,作GN⊥AB于N,EM⊥AB于M.
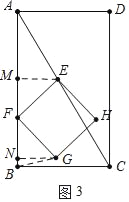
由△EMF≌△FNG,可得NG=FM=4﹣4t,
∴S=![]() FBGN=
FBGN=![]() 2t(4﹣4t)=﹣4t2+4t.
2t(4﹣4t)=﹣4t2+4t.
②如图4中,当1<t≤2时,作GN⊥AB于N,EM⊥AB于M.
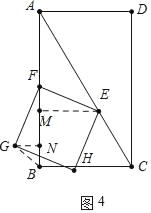
由△EMF≌△FNG,可得NG=FM=4t﹣4
S=![]()
![]() 2t(4t﹣4)=4t2﹣4t.
2t(4t﹣4)=4t2﹣4t.
综上所述,S=![]() .
.
(4)①如图5中,当H在BD的垂直平分线上时,
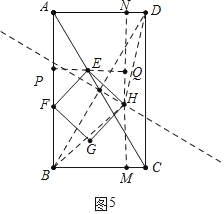
作HM⊥BC于M,延长MH交AD于N,作EP⊥AB于P,延长PE交MN于Q.
由△EPF≌△HQE可得HQ=EP=T.EQ=PF=4﹣4t,
在Rt△HND中,DH2=DN2+HN2=(3t﹣2)2+(3t)2,
在Rt△BHM中,BH2=(4﹣3t)2+(4﹣3t)2,
∴HD=HB,
∴(3t﹣2)2+(3t)2=4﹣3t)2+(4﹣3t)2,
∴t=![]() .
.
②当点E在BD的垂直平分线上时,易知AE=EC,t=1.
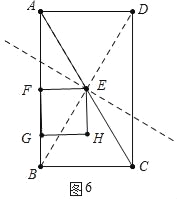
③当点F在线段BD的垂直平分线上时,
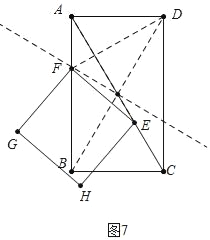
∵BF=DF=2t
在Rt△ADF中,22+(4﹣2t2=(2t)2,
∴t=![]() ,
,
综上所述,当正方形EFGH的顶点与点B,D距离相等时的t值为![]() s或1s或
s或1s或![]() s.
s.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
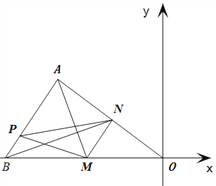
【题目】如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(-4,3),B(-6,0), O是原点.点M是OB边上异于O,B的一动点,过点M作MN//AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点![]() .
.
(1)求出OA所在直线的解析式,并求出点M的坐标为(-1,0)时,点N的坐标.
(2)若 ![]() =
=![]() 时,求此时点N的坐标.
时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,反映的是九(1)班学生外出乘车、步行、骑车的人数直方图的一部分和圆形分布图,下列说法:①九(1)班外出步行有8人;②在圆形统计图中,步行人数所占的圆心角度数为82°;
③九(1)班外出的学生共有40人;④若该校九年级外出的学生共有500人,那么估计全年级外出骑车的人约有150人,其中正确的结论是( )


A. ①②③ B. ①③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购进甲、乙两种规格的书柜.调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择,并求出最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:

(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对称变换和平移变换在平面几何中有着广泛的应用,特别是在解决有关最值问题时,更是我们常用的思维方法,请你利用所学知识解决下列问题:

(1)如图①,在平面直角坐标系中,已知点A(0,1),点B(2,1),点P在x轴上运动,当PA+PB的值最小时,点P的坐标是 ;(请直接写出答案)
(2)如图②,AD⊥l于点D,BC⊥l于点C,且AD=2,AB=BC=4,当点P在直线l上运动时,PA+PB的最小值是 ;(请直接写出答案)
(3)如图③,直线a∥b,且a与b之间的距离为1,点A到直线a的距离为2,点B到直线b的距离为2,且AB=![]() ,问:在直线a上是否存在点C,在直线b上是否存在点D,使得CD⊥a,且AC+CD+DB的值最小?若存在,请求出AC+CD+DB的最小值;若不存在,请说明理由.
,问:在直线a上是否存在点C,在直线b上是否存在点D,使得CD⊥a,且AC+CD+DB的值最小?若存在,请求出AC+CD+DB的最小值;若不存在,请说明理由.
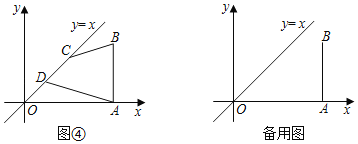
(4)如图④,在平面直角坐标系中,A(6,0),B(6,4),线段CD在直线y=x上运动,且CD=2![]() ,则四边形ABCD周长的最小值是 ,此时点D的坐标为 .(请直接写出答案)
,则四边形ABCD周长的最小值是 ,此时点D的坐标为 .(请直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com