练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．某快递公司有甲、乙两个仓库，各存有快件若干件，甲仓库发走80件后余下的快件数比乙仓库原有快件数的2倍少700件；乙仓库发走560件后剩余的快件数是甲仓库余下的快件数的$\frac{1}{5}$还多210件，求甲、乙两个仓库原有快件各多少件？

    分析 甲、乙两个仓库原有快件分别有x件和y件．构建题意列出方程组即可解决问题．

    解答 解：设甲、乙两个仓库原有快件分别有x件和y件．
    由题意$\left\{\begin{array}{l}{x-80=2y-700}\\{y-560=\frac{1}{5}（x-80）+210}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{x=1480}\\{y=1050}\end{array}\right.$，
    答：甲、乙两个仓库原有快件分别有1480件1050件

    点评 本题考查二元一次方程组的应用，解题的关键是学会设未知数，寻找等量关系，构建方程组解决问题，属于基础题，中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

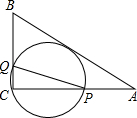    2．如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA，CB分别相交于点P，Q，则线段PQ的最小值（　　）
    A．5B．4$\sqrt{2}$C．4.75D．4.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算题：
    （1）（-12）+6+（-14）
    （2）-3-4+5
    （3）（$\frac{1}{2}$+$\frac{5}{6}$-$\frac{7}{12}$）×（-60）
    （4）（-9）÷$\frac{3}{2}$×$\frac{5}{6}$÷（-8）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．若2＜m＜8，化简：$\sqrt{{（2-m）}^{2}}$-$\sqrt{{（8-m）}^{2}}$=2m-10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．某工厂加工一批零件，为了提高工人工作积极性，工厂规定每名工人每次薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的是（　　）
    A．a=20
    B．b=4
    C．若工人甲一天获得薪金180元，则他共生产50件
    D．若工人乙一天生产m（件），则他获得薪金4m元

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，在△ABC中，∠ACB=90°，分别以点A，B为圆心，大于$\frac{1}{2}$AB长为半径作弧，两弧交于点M，N，作直线MN分别交AB，AC于点D，E，连结CD，BE，下列结论错误的是（　　）
    A．AD=CDB．BE＞CDC．∠BEC=∠BDCD．BE平分∠CBD

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

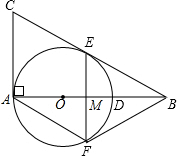    4．如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边AB相交于点D，与边BC相切于点E．
    （1）若AC=6，BC=10，求⊙O的半径．
    （2）过点E作弦EF⊥AB于M，连接AF，若AD=4，∠AFE=60°，
    ①求劣弧EF的长．②求弦EF的长，并说明四边形ACEF是什么特殊四边形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

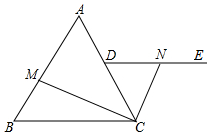    1．如图，在边长为6的等边△ABC中，D为AC中点，射线DE∥BC，M，N分别为线段AB与射线DE上的点，连结CM，CN，若BM=DN，则CM+CN的最小值为3$\sqrt{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在梯形ABCD中，AD∥BC，AE=DE，AC与BD相交于点E，∠ADB=60°，且BE：ED=3：1，BD=12，求梯形ABCD的周长．

    查看答案和解析>>

    同步练习册答案