
����Ŀ���ڡ�ABC�У���A=90�㣬AB=4��AC=3��M��AB�ϵĶ��㣨����A��B�غϣ�����M����MN��BC��AC�ڵ�N��
��1����ͼ1���ѡ�AMN��ֱ��MN�۵��õ���PMN����AM=x��
i������P�����ڱ�BC�ϣ���x��ֵ��
ii����M���˶������У��ǡ�MNP������BCNM�غϵ����Ϊy������y����x�ĺ�����ϵʽ������y�����ֵ��
��2����ͼ2����MNΪֱ������O�����ڡ�O�����ڽӾ���AMQN�����ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɣ�

���𰸡���1��i����x=2ʱ����Pǡ�����ڱ�BC�ϣ�ii�� y=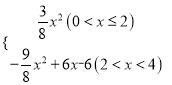 ����x=
����x=![]() ʱ���ص����ֵ���������ֵΪ2����2����x=
ʱ���ص����ֵ���������ֵΪ2����2����x=![]() ʱ����O��ֱ��BC���У���x��
ʱ����O��ֱ��BC���У���x��![]() ʱ����O��ֱ��BC���룻x��
ʱ����O��ֱ��BC���룻x��![]() ʱ����O��ֱ��BC�ཻ��
ʱ����O��ֱ��BC�ཻ��
�������������������1��i��������ԳƵ����ʣ��������ȵ��߶���ǣ��ɵõ�M��AB�е㣬����x=![]() AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
ii��������������ۣ�����0��x��2ʱ����MNP������BCNM�غϵ����Ϊ��MNP�������������ԳƵ�������MNP�����������AMN���������y=![]() x2
x2
����2��x��4ʱ����ͼ2����PM��PN�ֱ�BC��E��F����i��֪ME=MB=4-x��PE=PM-ME=x-��4-x��=2x-4��������֪��PEF�ס�ABC���������������ε����ʼ�����ã�
��2�����÷������۵�˼�룬�����ֱ��BC����O����ʱ��x��ֵ��Ȼ��õ��ཻ������ʱx��ȡֵ��Χ��
�����������1��i����ͼ1��
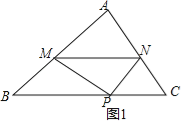
����Գ�����֪��AM=PM����AMN=��PMN��
��MN��BC��
���PMN=��BPM����AMN=��B��
���B=��BPM��
��AM=PM=BM��
����M��AB�е㣬����x=![]() AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
ii�����·�����������ۣ�
����0��x��2ʱ��
��MN��BC��
���AMN�ס�ABC��
��![]() ��
��
��![]() ��
��
��AN= ![]() ��
��
��MNP������BCNM�غϵ����Ϊ��MNP�������
��![]() ��
��
����2��x��4ʱ����ͼ2��
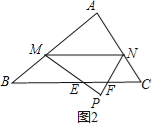
��PM��PN�ֱ�BC��E��F��
�ɣ�2��֪ME=MB=4-x��
��PE=PM-ME=x-��4-x��=2x-4��
������֪��PEF�ס�ABC��
��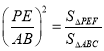 ��
��
��S��PEF=![]() ��x-2��2��
��x-2��2��
��y=S��PMN-S��PEF=![]() ��
��
����0��x��2ʱ��y=![]() x2��
x2��
����֪y���=![]() ��
��
������2��x��4ʱ��y=![]() ��
��
����x=![]() ʱ������2��x��4����y���=2��
ʱ������2��x��4����y���=2��
������������x=![]() ʱ���ص����ֵ���������ֵΪ2��
ʱ���ص����ֵ���������ֵΪ2��
��2������ͼ3��
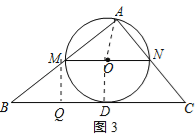
��ֱ��BC����O�����ڵ�D������AO��OD����AO=OD=![]() MN��
MN��
��Rt��ABC��BC=![]() =5��
=5��
�ɣ�1��֪��AMN�ס�ABC��
��![]() ����
����![]() ��
��
��MN=![]() x
x
��OD=![]() x��
x��
��M����MQ��BC��Q����MQ=OD=![]() x��
x��
��Rt��BMQ��Rt��BCA�У���B�ǹ����ǣ�
���BMQ�ס�BCA��
��![]() ��
��
��BM= ![]() ��AB=BM+MA=
��AB=BM+MA=![]() x+x=4
x+x=4
��x=![]() ��
��
����x=![]() ʱ����O��ֱ��BC���У�
ʱ����O��ֱ��BC���У�
��x��![]() ʱ����O��ֱ��BC���룻
ʱ����O��ֱ��BC���룻
x��![]() ʱ����O��ֱ��BC�ཻ��
ʱ����O��ֱ��BC�ཻ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��![]() x2+
x2+![]() x+4��x���ڵ�A��B����y���ڵ�C������AC��BC��
x+4��x���ڵ�A��B����y���ڵ�C������AC��BC��
��1����A��B�������Լ�ֱ��BC�Ľ���ʽ��
��2����ͼ1������P�ӵ�B������ÿ��5����λ���ٶ����O�˶�������P��y���ƽ���߽��߶�BC�ڵ�M�����������ڵ�N������N��NC��BC��BC�ڵ�K������MNK����MPB�������Ϊ1��2ʱ����P���˶�ʱ��t��ֵ��
��3����ͼ2������P �ӵ�B������ÿ��5����λ���ٶ����A�˶���ͬʱ��һ������Q�ӵ�A������AC����ͬ�ٶ����յ�C�˶�����P��Qͬʱֹͣ���ֱ���PQ��BPΪ����x���Ϸ���������PQEF��������BPGH�������ζ��㰴˳ʱ��˳����������PQEF��������BPGH�ص�������һ����Գ�ͼ��ʱ���������ʱ��Գ�ͼ�ε������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��m+3��m+1����x���ϣ���P�������Ϊ�� �� ��
A. ��0��1��B. ��1��0��C. ��0��-2��D. ��2��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ��ˮ�����̣�ij���乫˾�е���������Ϊ106m3����ʯ�����ù�˾�мס��������ͺŵĿ�����100�������ͳ�ƽ��ÿ�����������ʯ��80m3�����ͳ�ƽ��ÿ�����������ʯ��120m3���ƻ�100�������������
��1���ù�˾�ס��������ͺŵĿ������ж���̨��
��2������ù�˾��ԭ�е�100������������40������ڹ��̽��ȵ���Ҫ��ʣ�µ������������������50������ɣ��ڼ��Ϳ���������������£���˾����Ӧ���Ӷ��������Ϳ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������д���ʽ������:
(1)n��ʾ����,n(n+1)(n+2)��ʾ___________________________________.
(2)3x+5y��ʾ____________________________________________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
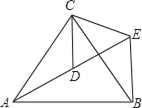
����Ŀ����ͼ����ACB����ECD���ǵȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��1����֤��AD=BE��
��2�����AEB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����kΪ������������993��99�ܱ�k��������k����������������
A. 50 B. 100 C. 98 D. 97
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵꽫ij�ַ�װ���ɱ������40%���ۣ�����8���Ż����������ÿ������װ�Կɻ���15Ԫ�������ַ�װÿ���ijɱ��ǣ� ��
A.120Ԫ
B.125Ԫ
C.135Ԫ
D.140Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ�ںڰ���д��һ����ʽ��(a��3)x��4(a��3)������˵x��4������˵��һ������x��4ʱ�������ʽҲ���ܳ�������ͬ��˭�Ĺ۵㣿���õ�ʽ�Ļ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com