
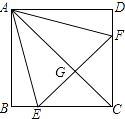
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE , 其中正确结论有( ) 
A.2个
B.3个
C.4个
D.5个
【答案】C
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
![]() ,
,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°(故②正确),
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故③正确).
设EC=x,由勾股定理,得
EF= ![]() x,CG=
x,CG= ![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°= ![]() x,
x,
∴AC= ![]() ,
,
∴AB= ![]() ,
,
∴BE= ![]() ﹣x=
﹣x= ![]() ,
,
∴BE+DF= ![]() x﹣x≠
x﹣x≠ ![]() x,(故④错误),
x,(故④错误),
∵S△CEF= ![]() x2,
x2,
S△ABE= ![]() x2,
x2,
∴2S△ABE= ![]() x2=S△CEF,(故⑤正确).
x2=S△CEF,(故⑤正确).
综上所述,正确的有4个,
故选:C.
通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC,就可以得出AC垂直平分EF,设EC=x,BE=y,由勾股定理就可以得出x与y的关系,表示出BE与EF,利用三角形的面积公式分别表示出S△CEF和2S△ABE,再通过比较大小就可以得出结论.


科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图. 
(1)试求y与x之间的函数关系式;
(2)若“康乃馨”的进价为5元/枝,且要求每枝的销售盈利不少于1元,问:在此次活动中,他们最多可购进多少数量的康乃馨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.
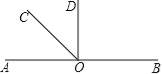
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线a:y=x+2和直线b:y=﹣x+4相交于点A,分别与x轴相交于点B和点C,与y轴相交于点D和点E.
(1)求△ABC的面积;
(2)求四边形ADOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.

(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,99999×11=1099989,99999×12=1199988,99999×13=1299987,99999×14=1399986,那么,99999×20= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com