
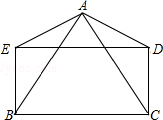
 如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.分析 (1)利用SAS证得两个三角形全等即可;
(2)要证明四边形BCED为矩形,则要证明四边形BCED是平行四边形,且对角线相等.
解答 (1)证明:∵∠BAD=∠CAE,
∴∠EAB=∠DAC,
在△ABE和△ACD中
∵AB=AC,∠EAB=∠DAC,AE=AD
∴△ABE≌△ACD(SAS);
(2)∵△ABE≌△ACD,
∴BE=CD,
又DE=BC,
∴四边形BCDE为平行四边形.
∵AB=AC,
∴∠ABC=∠ACB
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠EBC=∠DCB
∵四边形BCDE为平行四边形,
∴EB∥DC,
∴∠EBC+∠DCB=180°,
∴∠EBC=∠DCB=90°,
四边形BCDE是矩形.
点评 本题主要考查矩形的判定,证明对角线相等的平行四边形是矩形,解题的关键是熟练掌握矩形的判定方法.


科目:初中数学 来源: 题型:选择题
| A. | 不等边三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.83×107吨 | B. | 2.83×108吨 | C. | 2.83×109吨 | D. | 2.83×1010吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
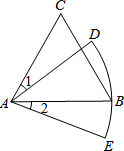 如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )| A. | 1π | B. | 1.5π | C. | 2π | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
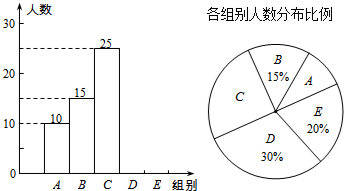 某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.| 组别 | 正常字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 5 | 10 | 5 | 15 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com