
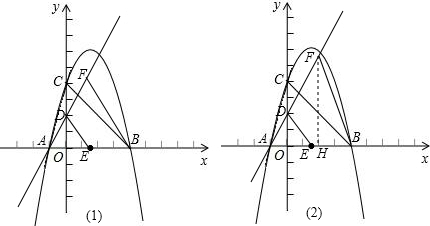
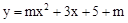 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.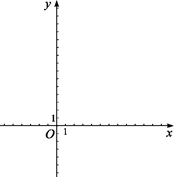
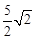 ?若存在,求出点G的坐标;若不存在请说明理由.
?若存在,求出点G的坐标;若不存在请说明理由.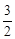 ,5);(3)(
,5);(3)(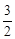 ,
,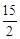 )或(
)或(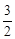 ,
,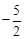 ).
).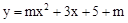 与y轴交于点C(0,4),把C点的坐标代入解析式建立方程,求出方程的解,就可以求出m的值;
与y轴交于点C(0,4),把C点的坐标代入解析式建立方程,求出方程的解,就可以求出m的值;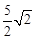 的直线的解析式,再由抛物线的对称轴与这些与BC平行的直线的解析式构建方程组求出其解,就可以求出G的坐标.
的直线的解析式,再由抛物线的对称轴与这些与BC平行的直线的解析式构建方程组求出其解,就可以求出G的坐标.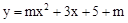 与y轴交于点C(0,4),
与y轴交于点C(0,4),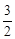 ,0).
,0).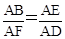 时,由于E为AB的中点,此时D为AF的中点,可求 F点坐标为(1,4).
时,由于E为AB的中点,此时D为AF的中点,可求 F点坐标为(1,4).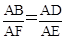 时,
时,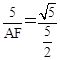 ,解得:
,解得: 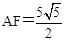 .
.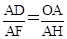 .
.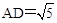 .
.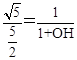 , 解得
, 解得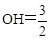 .
.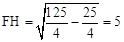 ,
,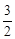 ,5).
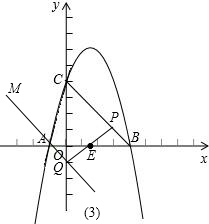
,5).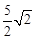 ,∴由勾股定理,得CQ=5.
,∴由勾股定理,得CQ=5.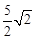 的直线为y=-x+9或y=-x-1.
的直线为y=-x+9或y=-x-1.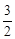 ,
,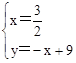 或
或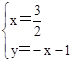 ,解得:
,解得: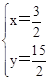 或
或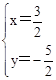 .
.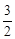 ,
,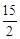 )或(
)或(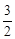 ,
,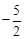 ).
).


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 为常数,且
为常数,且 .
. 为何值,该函数的图象与
为何值,该函数的图象与 轴总有两个公共点;
轴总有两个公共点; 轴交于A,B两点,当△ABC的面积等于2时,求
轴交于A,B两点,当△ABC的面积等于2时,求 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,匀减速行驶路程为
,匀减速行驶路程为 ,其中
,其中 、
、 为常数. 一汽车经过启动、匀加速行驶、匀速行驶、匀减速行驶之后停车,若把这一过程中汽车的行驶路程
为常数. 一汽车经过启动、匀加速行驶、匀速行驶、匀减速行驶之后停车,若把这一过程中汽车的行驶路程 看作时间
看作时间 的函数,其图象可能是( )
的函数,其图象可能是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com