
 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4.| m |
| x |
| m |
| x |
| m |
| x |
| m |
| x |
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 12 |
| 1 |
| 3 |
| x2-1 |
| x2+2x |
| x-1 |
| x |
| x |
| x+2 |
查看答案和解析>>
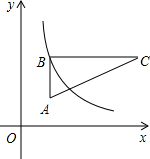
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 李师傅驾车到外地送货,出发前汽车油箱有50升油,行驶若干小时后,在加油站加油若干升后继续行驶.如图是表示汽车油箱中剩余油量y(单位:升)与行驶时间t(单位:时)之间函数关系的图象.请根据图象解答下列问题:
李师傅驾车到外地送货,出发前汽车油箱有50升油,行驶若干小时后,在加油站加油若干升后继续行驶.如图是表示汽车油箱中剩余油量y(单位:升)与行驶时间t(单位:时)之间函数关系的图象.请根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
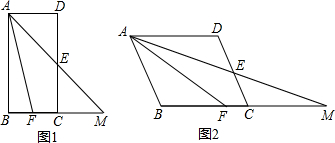
 如图,AB为圆O的直径,点C是圆O上一点,AC平分∠DAB,AD⊥CD,线段AB与DC的延长线交于点P.
如图,AB为圆O的直径,点C是圆O上一点,AC平分∠DAB,AD⊥CD,线段AB与DC的延长线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
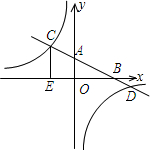 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
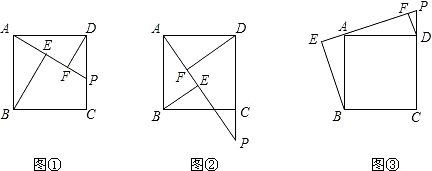
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度; ①将△ABC绕点C逆时针旋转90°得△A1B1C1,②作出△ABC关于点O的中心对称图形△A2B2C2,画出两个图形,并标明对应字母.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度; ①将△ABC绕点C逆时针旋转90°得△A1B1C1,②作出△ABC关于点O的中心对称图形△A2B2C2,画出两个图形,并标明对应字母.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com