Question

【题目】解答题
（1）如图1，在正方形ABCD中，点O是对角线AC的中点，点E是边BC上一点，连接OE，过点O作OE的垂线交AB于点F．求证：OE=OF．
（2）若将（1）中，“正方形ABCD”改为“矩形ABCD”，其他条件不变，如图2，连接EF． ⅰ）求证：∠OEF=∠BAC．
ⅱ）试探究线段AF，EF，CE之间数量上满足的关系，并说明理由．

Answer 1

【答案】
（1）证明：（1）连接OB，

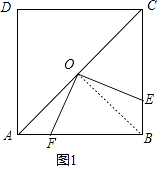
∵在正方形ABCD中，O是AC的中点，

∴OB=OA，∠OAB=∠OBA=∠OBC=45°，

∴∠AOB=90°，

又∵OE⊥OF，

∴∠AOF=∠BOE，

在△AOF和△BOE中， ，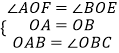

∴△AOF≌△BOE，

∴OE=OF；

（2）①∵∠EOF=∠FBE=90°，

∴O，E，F，B四点共圆，

∴∠OBA=∠OEF，

∵在矩形ABCD中，O是AC的中点，

∴OA=OB，∠OAB=∠OBA，

∴∠OEF=∠BAC；

②如图，连接BD，延长EO交AD于G，

∵BD与AC交于O，

则△OGD≌△DEB，

∴OG=OE，

∴AG=CE，

∵OF⊥GE，

∴FG=EF，

在Rt△AGF中，GF2=AG2+AF2，即EF2=CE2+AF2．

【解析】（1）连接OB，更好正方形的性质得到OB=OA，∠OAB=∠OBA=∠OBC=45°，得到∠AOB=90°，根据全等三角形的判定和性质即可得到结论；（2）①根据已知条件得到O，E，F，B四点共圆，由圆周角定理得到∠OBA=∠OEF，根据矩形的性质即可得到结论；②如图，连接BD，延长EO交AD于G于是到OG=OE，根据线段的垂直平分线的性质得到FG=EF，根据勾股定理即可得到结论．
【考点精析】根据题目的已知条件，利用矩形的性质和正方形的性质的相关知识可以得到问题的答案，需要掌握矩形的四个角都是直角，矩形的对角线相等；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．