
����Ŀ��ij�������ӵļ۸�ΪaԪ/ǧ�ˣ����һ�ι���2ǧ�����ϵ����ӣ�����2ǧ�˲��ֵ����Ӽ۸��8�ۣ��±��ǹ�����x��ǧ�ˣ���������y��Ԫ�����ֶ�Ӧ��ֵ�������ϱ���
������x��ǧ�ˣ� | 1.5 | 2 | 2.5 | 3 |
������y��Ԫ�� | 7.5 | 10 | 12 | b |
��1��д��a��b��ֵ��a=�� �� b=�� ����
��2�������x��2ʱ��y����x�ĺ�����ϵʽ��
��3����ũ����18.8ԪǮȫ�����ڹ�����������ӣ��������Ĺ�������
���𰸡���1��5,14����2��y=4x+2����3����ũ���Ĺ�����Ϊ4.2ǧ�ˣ�
��������
��1���ɱ��ɵó�������Ϊ�������Ա���x���ٸ��ݹ���2ǧ�˻���10ԪǮ���ɵó�aֵ����ϳ���2ǧ�˲��ֵ����Ӽ۸��8�ۿɵó�bֵ��
��2���赱x��2ʱ��y����x�ĺ�������ʽΪy=kx+b�����ݵ���������ô���ϵ�������������������ʽ��
��3����18.8��10��������������=Ǯ���µ��������ɵó���ũ���Ĺ����ˣ��ٽ�y=18.8���루2���Ľ���ʽ�м������ũ���Ĺ�������
�⣺��1���ɱ��ɵó��������Ǻ������Ա���x��
��10��2=5��
��a=5��b=2��5+5��0.8=14��
�ʴ�Ϊ��5��14��
��2���赱x��2ʱ��y����x�ĺ�������ʽΪy=kx+b��
���㣨2.5��12������3��14������y=kx+b�У�
�ã�![]() ��
��
��ã�![]() ��
��
�൱x��2ʱ��y����x�ĺ�������ʽΪy=4x+2��
��3����18.8��10��
4x+2=18.8
x=4.2
���ũ���Ĺ�����Ϊ��4.2��ǧ�ˣ���
�𣺼�ũ���Ĺ�����Ϊ4.2ǧ�ˣ�


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���E�ڱ�CD�ϣ����þ�����AE�۵���ʹ��D���ڱ�BC�ϵĵ�F��������F���֡�FG��CD����AE�ڵ�G����DG��
��1����֤���ı���DEFGΪ���Σ�
��2����CD=8��CF=4����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx�ĶԳ���Ϊx=![]() ���Ҿ�����A��2��1������P���������ϵĶ��㣬P�ĺ�����Ϊm��0��m��2��������P��PB��x�ᣬ����ΪB��PB��OA�ڵ�C����O����ֱ��PB�ĶԳƵ�ΪD������CD��AD������A��AE��x�ᣬ����ΪE��
���Ҿ�����A��2��1������P���������ϵĶ��㣬P�ĺ�����Ϊm��0��m��2��������P��PB��x�ᣬ����ΪB��PB��OA�ڵ�C����O����ֱ��PB�ĶԳƵ�ΪD������CD��AD������A��AE��x�ᣬ����ΪE��
��1���������ߵĽ���ʽ;
��2����գ�
���ú�m��ʽ�ӱ�ʾ��C��D�����꣺
C���� ���� ������D���� �� ����
�ڵ�m=�� ��ʱ����ACD���ܳ���С��
��3������ACDΪ���������Σ�������з��������ĵ�P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���OBCD�е����������ڡ�O�ϣ���A�ǡ�O�ϵ�һ�����㣨�����B��C��D�غϣ������ı���OBCD��ƽ���ı���ʱ����ô��OBA�͡�ODA��������ϵ�� �� 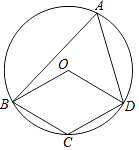
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�����ԭ��![]() ������������.����.����.���ҵķ�������ƽ�ƣ�ÿ���ƶ�һ����λ���õ�
������������.����.����.���ҵķ�������ƽ�ƣ�ÿ���ƶ�һ����λ���õ�![]() ��0��1����
��0��1����![]() ��1��1����
��1��1����![]() ��1��0����
��1��0����![]() ��2��0��������ô��
��2��0��������ô��![]() ������Ϊ__________.
������Ϊ__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��ν��ȫƽ��ʽ�����Ƕ���һ����ʽA�����������һ����ʽB��ʹ��A=B2 �� ���A����ȫƽ��ʽ������a4=��a2��2 �� 4a2��4a+1=��2a��1��2 ��
��1�����и�ʽ����ȫƽ��ʽ�ı����________��
��a6����a2+ab+b2����x2��4x+4y2��m2+6m+9����x2��10x��25����4a2+2ab+![]() ��
��
��2����4x2+xy+my2��x2��nxy+64y2������ȫƽ��ʽ����m2015n2016��ֵ��
��3������ʽ49x2+1����һ������ʽ��ʹ���ܳ�Ϊһ����ȫƽ��ʽ����ô���ϵĵ���ʽ��������Щ���������г����п��ܵ������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij��ѧ���꼶��ѧ�С��ѡ������ѧУǰ��С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30�㣬����������������6�����µ�A������A����ô�������B��������48�㣮��б��FA���±�i=1�� ![]() ��������ĸ߶ȣ����������һλС�����ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��
��������ĸ߶ȣ����������һλС�����ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11�� ![]() ȡ1.73��
ȡ1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���쳵������ͬʱ�Ӽס������س��������ҵغͼأ�������ʻ���쳵�����ҵغ���Ϣһ��Сʱ��ԭ�ٷ��أ������ڿ쳵ǰһ��Сʱ����أ���ͼ��ʾ������ʻ��������ص�·��y��km�������ʱ��x��h���ĺ���ͼ������ͼ�е���Ϣ������������⣺

��1���ס������صľ���Ϊ�� ��km���������ٶ�Ϊ�� ��km/h���쳵���ٶ�Ϊ�� ��km/h��
��2����ͼ���л����쳵��ص�·��y��km�������ʱ��x��h���ĺ���ͼ���������ע�����ֵ����
��3��������ʱ�䣬�������150km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������
��1����ͼ1����������ABCD�У���O�ǶԽ���AC���е㣬��E�DZ�BC��һ�㣬����OE������O��OE�Ĵ��߽�AB�ڵ�F����֤��OE=OF�� 
��2��������1���У���������ABCD����Ϊ������ABCD���������������䣬��ͼ2������EF�� ������֤����OEF=��BAC��
������̽���߶�AF��EF��CE֮������������Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com