
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=![]() ,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
(1)求抛物线的解析式;
(2)填空:
①用含m的式子表示点C,D的坐标:
C( , ),D( , );
②当m= 时,△ACD的周长最小;
(3)若△ACD为等腰三角形,求出所有符合条件的点P的坐标.
【答案】
(1)
解:(1)依题意,得 ,解得
,解得
∴y=x2﹣![]() x
x
(2)m;![]() ;2m;0;1
;2m;0;1
(3)
依题意,得B(m,0)
在RT△OBC中,OC2=OB2+BC2=m2+![]() =
=![]() m2,
m2,
∴OC=![]() m 又∵O,D关于直线PC对称,
m 又∵O,D关于直线PC对称,
∴CD=OC=![]() m
m
在RT△AOE中,OA=![]() =
=![]() =
=![]()
∴AC=OA﹣OC=![]() ﹣
﹣![]() m
m
在RT△ADE中,AD2=AE2+DE2=12+(2﹣2m)2=4m2﹣8m+5
分三种情况讨论:
①若AC=CD,即![]() ﹣
﹣![]() m=
m=![]() m,解得m=1,∴P(1,
m,解得m=1,∴P(1,![]() )
)
②若AC=AD,则有AC2=AD2,即5﹣5m+![]() m2=4m2﹣8m+5
m2=4m2﹣8m+5
解得m1=0,m2=![]() .∵0<m<2,∴m=
.∵0<m<2,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )
)
③若DA=DC,则有DA2=DC2,即4m2﹣8m+5=![]() m2
m2
解得m1=![]() ,m2=2,∵,0<m<2,∴m=
,m2=2,∵,0<m<2,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )
)
综上所述,当△ACD为等腰三角形是,点P的坐标分别为P1(1,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ).
).
【解析】(1)根据抛物线对称轴公式和代入法可得关于a,b的方程组,解方程组可得抛物线的解析式;
(2)①设OA所在的直线解析式为y=kx,将点A(2,1)代入求得OA所在的解析式为y=![]() x,因为PC⊥x轴,所以C得横坐标与P的横坐标相同,为m,令x=m,则y=
x,因为PC⊥x轴,所以C得横坐标与P的横坐标相同,为m,令x=m,则y=![]() m,所以得出点C(m,
m,所以得出点C(m,![]() m),又点O、D关于直线PB的对称,所以由中点坐标公式可得点D的横坐标为2m,则点D的坐标为(2m,0);
m),又点O、D关于直线PB的对称,所以由中点坐标公式可得点D的横坐标为2m,则点D的坐标为(2m,0);
②因为O与D关于直线PB的对称,所以PB垂直平分OD,则CO=CD,因为,△ACD的周长=AC+CD+AD=AC+CO+AD=AO,OA=![]() =
=![]() =
=![]() ,所以当AD最小时,△ACD的周长最小;根据垂线段最短,可知此时点D与E重合,其横坐标为2,故m=1.
,所以当AD最小时,△ACD的周长最小;根据垂线段最短,可知此时点D与E重合,其横坐标为2,故m=1.
(3)由中垂线得出CD=OC,再将OC、AC、AD用m表示,然后分情况讨论分别得到关于m的方程,解得m,再根据已知条件选取复合体艺的点P坐标即可.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
A.ac+1=b
B.ab+1=c
C.bc+1=a
D.以上都不是
查看答案和解析>>
科目:初中数学 来源: 题型:
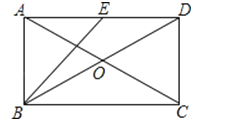
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=![]() ,则BO= ,∠EBD的大小约为 度 分.(参考数据:tan26°34′≈
,则BO= ,∠EBD的大小约为 度 分.(参考数据:tan26°34′≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形网格中,三角形的三个顶点均落在格点上.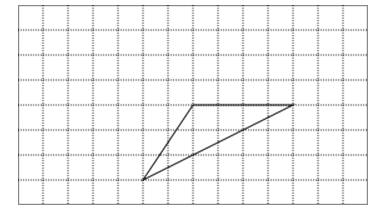
(1)以三角形的其中两边为边画一个平行四边形,并在顶点处标上字母A,B,C,D
(2)证明四边形ABCD是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.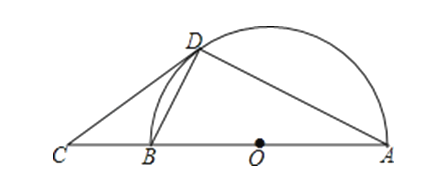
(1)求证:∠BAD=∠BDC;
(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.下表是购买量x(千克)、付款金额y(元)部分对应的值,请你结合表格:
购买量x(千克) | 1.5 | 2 | 2.5 | 3 |
付款金额y(元) | 7.5 | 10 | 12 | b |
(1)写出a、b的值,a= b= ;
(2)求出当x>2时,y关于x的函数关系式;
(3)甲农户将18.8元钱全部用于购买该玉米种子,计算他的购买量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com