
【题目】阅读理解:所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使得A=B2 , 则称A是完全平方式,例如a4=(a2)2 , 4a2﹣4a+1=(2a﹣1)2 .
(1)下列各式中完全平方式的编号有________;
①a6;②a2+ab+b2;③x2﹣4x+4y2④m2+6m+9;⑤x2﹣10x﹣25;⑥4a2+2ab+![]() .
.
(2)若4x2+xy+my2和x2﹣nxy+64y2都是完全平方式,求m2015n2016的值;
(3)多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写出答案)
【答案】(1)①④⑥(2)16;(3)见解析.
【解析】
(1)将各式先变形,利用完全平方式的结构特征判断即可;
(2)利用完全平方公式的结构特征求出m与n的值,代入原式计算即可得到结果;
(3)可将给出的两项看作完全平方式的前两项或第一项和第三项,分别求得第三项和第二项,而给出的二项式的两项本身都是完全平方式,还可去掉其中一项,由此即可得解。
(1)①④⑥
(2)解:∵4x2+xy+my2和x2﹣mxy+64y2都是完全平方式,
∴m=![]() ,n=±16,
,n=±16,
则原式=(![]() ×16)2015×16=16;
×16)2015×16=16;
(3)解:多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是14x,﹣14x,﹣1,﹣49x2 , ![]() .
.


科目:初中数学 来源: 题型:
【题目】为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】萧山北干初中组织外国教师(外教)进班上英语课,王明同学为了解全校学生对外教的喜爱程度,在全校随机抽取了若干名学生进行问卷调查.问卷将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢)、D(很不喜欢)四种类型,根据调查结果绘制成了两幅不完整的统计图,请结合统计图信息解答下列问题: 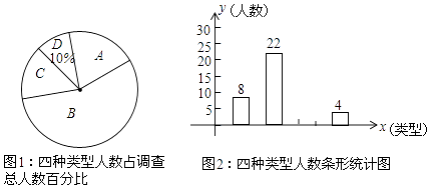
(1)这次调查中,一共调查了名学生,图1中C类所对应的圆心角度数为;
(2)请补全条形统计图;
(3)在非常喜欢外教的5位同学(三男两女)中任意抽取两位同学作为交换生,请用列表法或画树状图求出恰好抽到一名男生和一名女生作为交换生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.下表是购买量x(千克)、付款金额y(元)部分对应的值,请你结合表格:
购买量x(千克) | 1.5 | 2 | 2.5 | 3 |
付款金额y(元) | 7.5 | 10 | 12 | b |
(1)写出a、b的值,a= b= ;
(2)求出当x>2时,y关于x的函数关系式;
(3)甲农户将18.8元钱全部用于购买该玉米种子,计算他的购买量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为![]() 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=![]() =
=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴BF=![]() .
.
∴BC:BF=1:![]() =
=![]() :1.
:1.
∴四边形BCEF为![]() 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;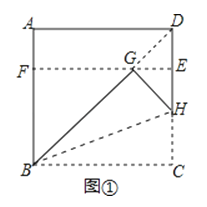
(2)已知四边形BCEF为![]() 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是![]() 矩形;
矩形;
(3)将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,则n的值是 .
矩形”,则n的值是 .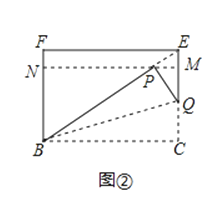
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:
第一步,分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步,从左边一堆拿出两张,放入中间一堆;
第三步,从右边一堆拿出一张,放入中间一堆;
第四步,左边一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数,聪明的你,你认为中间一堆牌的张数是多少?
【答案】5
【解析】
此题看似复杂,其实只是考查了整式的基本运算.把每堆牌的数量用相应的字母表示出来,列式表示变化情况即可找出最后答案.
解答:解:设第一步时候,每堆牌的数量都是x(x≥2);
第二步时候:左边x-2,中间x+2,右边x;
第三步时候:左边x-2,中级x+3,右边x-1;
第四步开始时候,左边有(x-2)张牌,则从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5.
所以中间一堆牌此时有5张牌.
【题型】填空题
【结束】
44
【题目】为什么总是1 089?
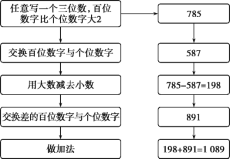
用不同的三位数再试几次,结果都是1 089吗?你能发现其中的原因吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com