
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为![]() 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=![]() =
=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴BF=![]() .
.
∴BC:BF=1:![]() =
=![]() :1.
:1.
∴四边形BCEF为![]() 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;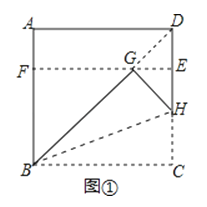
(2)已知四边形BCEF为![]() 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是![]() 矩形;
矩形;
(3)将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,则n的值是 .
矩形”,则n的值是 .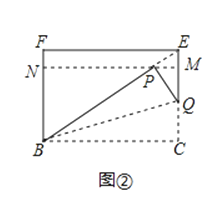
【答案】
(1)GH、DG;![]()
(2)
∵BC=1,EC=BF=![]() ,
,
∴BE=![]() =
=![]() .
.
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴![]() =
=![]() ,即BPBF=BEBN,
,即BPBF=BEBN,
∴1×![]() =
=![]() BN,
BN,
∴BN=![]() ,
,
∴BC:BN=1:![]() =
=![]() :1,
:1,
∴四边形BCMN是![]() 的矩形;
的矩形;
(3)6
【解析】(1)由折叠可得:
DG=HG,GH=CH,
∴DG=GH=CH.
设HC=x,则DG=GH=x.
∵∠DGH=90°,∴DH=![]() x,
x,
∴DC=DH+CH=![]() x+x=1,
x+x=1,
解得x=![]() .
.
∴tan∠HBC=![]() =
=![]() =
=![]() .
.
所以答案是:GH、DG,![]()
(3)同理可得:
将![]() 矩形沿用(2)中的方式操作1次后,得到一个“
矩形沿用(2)中的方式操作1次后,得到一个“![]() 矩形”,
矩形”,
将![]() 矩形沿用(2)中的方式操作1次后,得到一个“
矩形沿用(2)中的方式操作1次后,得到一个“![]() 矩形”,
矩形”,
将![]() 矩形沿用(2)中的方式操作1次后,得到一个“
矩形沿用(2)中的方式操作1次后,得到一个“![]() 矩形”,
矩形”,
所以将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,
矩形”,
所以答案是6.
【考点精析】根据题目的已知条件,利用勾股定理的概念和正方形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】阅读理解
抛物线y=![]() x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y=![]() x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.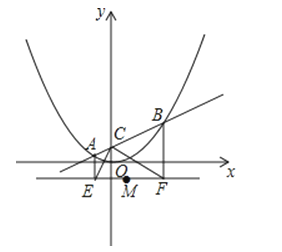
(1)写出点C的坐标,并说明∠ECF=90°
(2)在△PEF中,M为EF中点,P为动点.
①求证:PE2+PF2=2(PM2+EM2);
②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C,则:
①a+c=0;
②无论a取何值,此二次函数图象与x轴必有两个交点,函数图象截x轴所得的线段长度必大于2;
③当函数在x< ![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当﹣1<m<n<0时,m+n< ![]() ;
;
⑤若a=1,则OAOB=OC2 .
以上说法正确的有( )
A.①②③④⑤
B.①②④⑤
C.②③④
D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P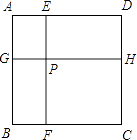
(1)若AG=AE,证明:AF=AH;
(2)若矩形PFCH的面积,恰矩形AGPE面积的两倍,试确定∠HAF的大小;
(3)若矩形EPHD的面积为 ![]() ,求Rt△GBF的周长.
,求Rt△GBF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使得A=B2 , 则称A是完全平方式,例如a4=(a2)2 , 4a2﹣4a+1=(2a﹣1)2 .
(1)下列各式中完全平方式的编号有________;
①a6;②a2+ab+b2;③x2﹣4x+4y2④m2+6m+9;⑤x2﹣10x﹣25;⑥4a2+2ab+![]() .
.
(2)若4x2+xy+my2和x2﹣nxy+64y2都是完全平方式,求m2015n2016的值;
(3)多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
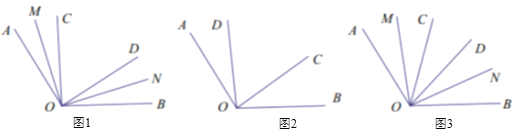
【题目】已知![]() 在
在![]() 的内部,OM平分
的内部,OM平分![]() ,ON平分
,ON平分![]()
(1)如图1,![]() 时,当OC在OD的左侧,求
时,当OC在OD的左侧,求![]() 的度数.
的度数.
(2)如图2,![]() 时,当OC在OD的右侧 ,请补全图形,并求
时,当OC在OD的右侧 ,请补全图形,并求![]() 的度数.
的度数.
(3)如图3,当![]() ,且OC在OD左侧时,试用
,且OC在OD左侧时,试用![]() 的代数式表示
的代数式表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数y= ![]() 经过正方形AOBC对角线的交点,半径为(6﹣3
经过正方形AOBC对角线的交点,半径为(6﹣3 ![]() )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 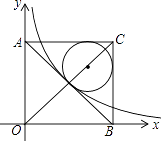
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.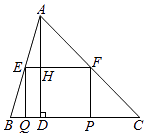
(1)求证: ![]() =
= ![]() ;
;
(2)设EF的长为x.
①当x为何值时,矩形EFPQ为正方形?
②当x为何值时,矩形EFPQ的面积最大?并求其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.
x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线y=﹣ ![]() x+3平行,求直线l的解析式.
x+3平行,求直线l的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com