
【题目】如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.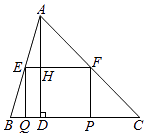
(1)求证: ![]() =
= ![]() ;
;
(2)设EF的长为x.
①当x为何值时,矩形EFPQ为正方形?
②当x为何值时,矩形EFPQ的面积最大?并求其最大值.
【答案】
(1)
解:证明:∵四边形EFPQ是矩形,
∴EF∥BC,
∴△AEF∽△ABC,∠AHF=∠ADC,
又∵AD是高,
∴∠AHF=∠ADC=90°,即AH是△AEF的高.
∴ ![]() ;
;
(2)
解:①若矩形EFPQ为正方形,则HD=EQ=EF=x.
∴AH=AD﹣HD=8﹣x.
又∵ ![]() ,BC=10,
,BC=10,
∴ ![]() .
.
解得 ![]() .
.
∴当 ![]() 时,矩形EFPQ为正方形;
时,矩形EFPQ为正方形;
②∵HD=EQ,AD=8,
∴AH=AD﹣HD=8﹣EQ.
又∵ ![]() ,EF=x,BC=10,
,EF=x,BC=10,
∴ ![]() .
.
∴ ![]() .
.
∴S矩形EFPQ= ![]() .
.
∵S矩形EFPQ= ![]() (0<x<10),
(0<x<10),
∴当x=5时,S矩形EFPQ有最大值为20.
∴当x=5时,矩形EFPQ的面积最大,最大面积为20
【解析】(1)根据矩形的性质得出EQ=HD=FP,EF∥BC,推出△AEF∽△ABC,根据相似三角形的性质推出即可;(2)①根据正方形的性质可知HD=EQ=EF,令HD=EQ=EF=x;利用相似三角形的性质可得 ![]() ,可得x的值;②根据矩形的面积公式,可以把面积表示成关于EF的长的函数,根据函数的性质即可求解.
,可得x的值;②根据矩形的面积公式,可以把面积表示成关于EF的长的函数,根据函数的性质即可求解.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


科目:初中数学 来源: 题型:
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3 ![]() ﹣3,CD∥AB,并与弧AB相交于点M、N.
﹣3,CD∥AB,并与弧AB相交于点M、N. 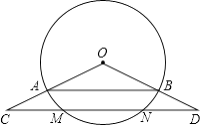
(1)求线段OD的长;
(2)若sin∠C= ![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为![]() 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=![]() =
=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴BF=![]() .
.
∴BC:BF=1:![]() =
=![]() :1.
:1.
∴四边形BCEF为![]() 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;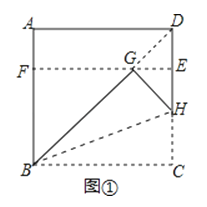
(2)已知四边形BCEF为![]() 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是![]() 矩形;
矩形;
(3)将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,则n的值是 .
矩形”,则n的值是 .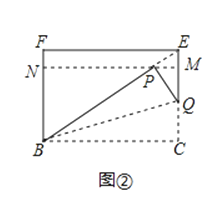
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力 | 科研能力 | 组织能力 | |
甲 | 81 | 85 | 86 |
乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.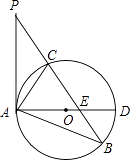
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长;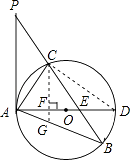
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是学习一元一次方程应用时,老师出示的问题和两名同学所列的方程,根据图中信息,解答下列问题.

(1)小杰同学所列方程中的x表示什么,小婷同学所列方程中的y表示什么;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么 ![]() 的值是 .
的值是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com