
【题目】如图是学习一元一次方程应用时,老师出示的问题和两名同学所列的方程,根据图中信息,解答下列问题.

(1)小杰同学所列方程中的x表示什么,小婷同学所列方程中的y表示什么;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题。
【答案】(1)x表示所买蓝布料的长度,y表示买蓝布料的费用;(2)(小杰)买蓝布料的费用+买黑布料的费用540元;(小婷)蓝布料的长度+黑布料的长度138m;(3)蓝布料买了75m ,黑布料买了63m。
【解析】
(1)根据两人的方程思路,可得出:x表示所买蓝布料的长度,y表示买蓝布料的费用;
(2)根据题意,可找出:(小杰)买蓝布料的费用+买黑布料的费用540元;(小婷)蓝布料的长度+黑布料的长度138m;
(3)选择两个方程中的一个,解之即可得出结论.
(1)所买蓝布料的长度,买蓝布料的费用;
(2)(小杰)买蓝布料的费用+买黑布料的费用=540元;
(小婷)蓝布料的长度+黑布料的长度=138m.
(3)选小杰的方程:3x+5(138-x)=540
解得:x=75 138![]()
答:蓝布料买了75m ,黑布料买了63m。
选小婷的方程:![]() =138
=138
解得y=225 540![]() 315
315
225÷3=75(m) 315÷5=63(m)
答:蓝布料买了75m ,黑布料买了63m。


科目:初中数学 来源: 题型:
【题目】如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P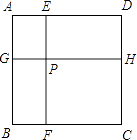
(1)若AG=AE,证明:AF=AH;
(2)若矩形PFCH的面积,恰矩形AGPE面积的两倍,试确定∠HAF的大小;
(3)若矩形EPHD的面积为 ![]() ,求Rt△GBF的周长.
,求Rt△GBF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.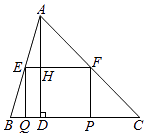
(1)求证: ![]() =
= ![]() ;
;
(2)设EF的长为x.
①当x为何值时,矩形EFPQ为正方形?
②当x为何值时,矩形EFPQ的面积最大?并求其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴相交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).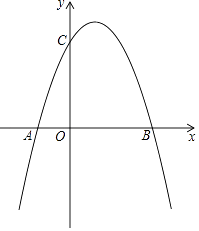
(1)求抛物线的解析式;
(2)连接BC,点P为抛物线上第一象限内一动点,当△BCP面积最大时,求点P的坐标;
(3)设点D是抛物线的对称轴上的一点,在抛物线上是否存在点Q,使以点B,C,D,Q为顶点的四边形为平行四边形?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.
x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线y=﹣ ![]() x+3平行,求直线l的解析式.
x+3平行,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P在对角线AC上,E在AC的延长线上,PB=PM , DE=EF.
(1)求证:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的长;
(3)如图2,若BF=10,△QCF是以CF为底的等腰三角形,连接DQ , 试求△CDQ的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com