
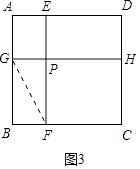
【题目】如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P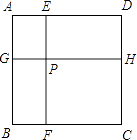
(1)若AG=AE,证明:AF=AH;
(2)若矩形PFCH的面积,恰矩形AGPE面积的两倍,试确定∠HAF的大小;
(3)若矩形EPHD的面积为 ![]() ,求Rt△GBF的周长.
,求Rt△GBF的周长.
【答案】
(1)
解:证明:如图1中,连接AF、AH,
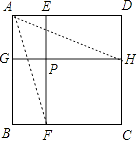
由题意知四边形AGHD与四边形AEFB均为矩形,
∴AG=DH,AE=BF,
∵AG=AE,
∴DH=BF,
∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ADH与Rt△ABF中,
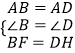 ,
,
∴△ABF≌△ADH,
∴AF=AH;
(2)
解:结论:∠HAF=45°.
理由:设AG=a,BG=b,AE=x,ED=y.
则 ![]() ,
,
∴a﹣x=y﹣b,两边平方得a2﹣2ax+x2=y2﹣2yb+b2,
∴得a2﹣2ax+x2=y2﹣4ax+b2,
∴(a+x)2=y2+b2,
∵y2+b2=FH2,
∴a+x=FH,
∵AG=DH=a,AE=BF=x,
∴DH+BF=FH,
延长FB到M,使得BM=DH,连接AM,
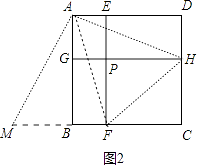
∵AD=AB,∠D=∠ABM,DH=BM,
∴△ADH≌△ABM,
∴AH=AM,∠DAH=∠BAM,
∴∠MAH=∠BAD=90°,
∵AF=AF,AM=AH,FM=FH,
∴△AFM≌△AFH,
∴∠FAH=∠FAM=45°
(3)
解:如图3中,连接GF,设BC=x,BF=y,则FG= ![]() ,
,
∴(x﹣1)(y﹣1)= ![]() ,∴xy﹣x﹣y+1=
,∴xy﹣x﹣y+1= ![]() ,∴xy﹣x﹣y=﹣
,∴xy﹣x﹣y=﹣ ![]()
∴x2+y2=x2+y2+1+2xy﹣2x﹣2y,
∴ ![]() =1﹣x﹣y,
=1﹣x﹣y,
得x+y+ ![]() =1,
=1,
∴Rt△GBF的周长=1.
【解析】(1)如图1中,连接AF、AH,由题意知四边形AGHD与四边形AEFB均为矩形,只要证明△ABF≌△ADH即可.(2)结论:∠HAF=45°.设AG=a,BG=b,AE=x,ED=y.由 ![]() ,推出(a+x)2=y2+b2 , 由y2+b2=FH2 , 推出a+x=FH,由AG=DH=a,AE=BF=x,推出DH+BF=FH,延长FB到M,使得BM=DH,连接AM,只要证明△ADH≌△ABM即可解决问题.(3)如图3中,连接GF,设BC=x,BF=y,则FG=
,推出(a+x)2=y2+b2 , 由y2+b2=FH2 , 推出a+x=FH,由AG=DH=a,AE=BF=x,推出DH+BF=FH,延长FB到M,使得BM=DH,连接AM,只要证明△ADH≌△ABM即可解决问题.(3)如图3中,连接GF,设BC=x,BF=y,则FG= ![]() ,由(x﹣1)(y﹣1)=
,由(x﹣1)(y﹣1)= ![]() ,推出xy﹣x﹣y+1=
,推出xy﹣x﹣y+1= ![]() ,推出xy﹣x﹣y=﹣
,推出xy﹣x﹣y=﹣ ![]() 推出x2+y2=x2+y2+1+2xy﹣2x﹣2y,推出
推出x2+y2=x2+y2+1+2xy﹣2x﹣2y,推出 ![]() =1﹣x﹣y,得x+y+
=1﹣x﹣y,得x+y+ ![]() =1,延长即可解决问题.
=1,延长即可解决问题.
【考点精析】通过灵活运用矩形的性质和正方形的性质,掌握矩形的四个角都是直角,矩形的对角线相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】理解:数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=![]() .tanD=tan15°=
.tanD=tan15°=![]() =
=![]() =2﹣
=2﹣![]() .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=![]() .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=![]() =
=![]() =2﹣
=2﹣![]() .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).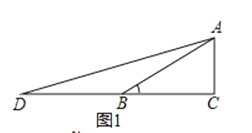
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线y=![]() x﹣1与双曲线y=
x﹣1与双曲线y=![]() 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.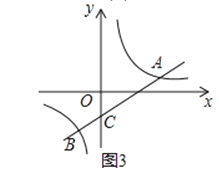
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3 ![]() ﹣3,CD∥AB,并与弧AB相交于点M、N.
﹣3,CD∥AB,并与弧AB相交于点M、N. 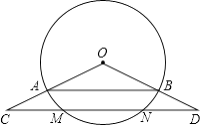
(1)求线段OD的长;
(2)若sin∠C= ![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
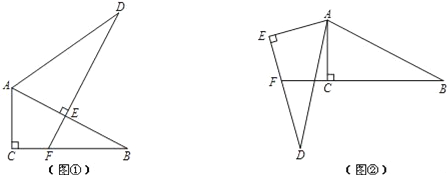
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】萧山北干初中组织外国教师(外教)进班上英语课,王明同学为了解全校学生对外教的喜爱程度,在全校随机抽取了若干名学生进行问卷调查.问卷将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢)、D(很不喜欢)四种类型,根据调查结果绘制成了两幅不完整的统计图,请结合统计图信息解答下列问题: 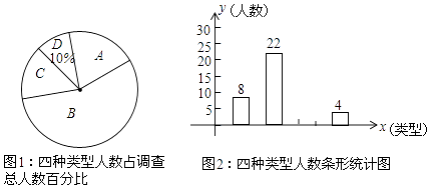
(1)这次调查中,一共调查了名学生,图1中C类所对应的圆心角度数为;
(2)请补全条形统计图;
(3)在非常喜欢外教的5位同学(三男两女)中任意抽取两位同学作为交换生,请用列表法或画树状图求出恰好抽到一名男生和一名女生作为交换生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() ,半径为2的⊙C,分别交AC,BC于点D,E,得到
,半径为2的⊙C,分别交AC,BC于点D,E,得到![]() .
. 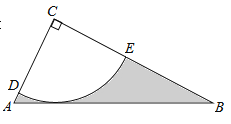
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为![]() 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=![]() =
=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴BF=![]() .
.
∴BC:BF=1:![]() =
=![]() :1.
:1.
∴四边形BCEF为![]() 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;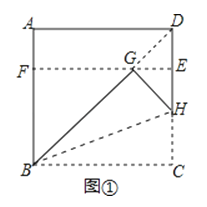
(2)已知四边形BCEF为![]() 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是![]() 矩形;
矩形;
(3)将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,则n的值是 .
矩形”,则n的值是 .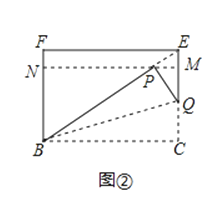
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是学习一元一次方程应用时,老师出示的问题和两名同学所列的方程,根据图中信息,解答下列问题.

(1)小杰同学所列方程中的x表示什么,小婷同学所列方程中的y表示什么;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com