
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() ,半径为2的⊙C,分别交AC,BC于点D,E,得到
,半径为2的⊙C,分别交AC,BC于点D,E,得到![]() .
. 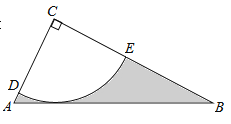
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
【答案】
(1)
证明:过点C作CH⊥AB于H,如图,
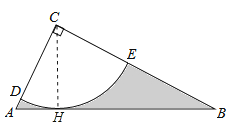
在Rt△ABC中,∵tanB=![]() =
=![]() ,
,
∴BC=2AC=![]() ,
,
∴AB=![]() =
=![]() =5,
=5,
∵![]() CHAB=
CHAB=![]() ACBC,
ACBC,
∴CH=![]() =2,
=2,
∵⊙C的半径为2,
∴CH为⊙C的半径,
而CH⊥AB,
∴AB为⊙C的切线;
(2)
解:S阴影部分=S△ACB﹣S扇形CDE
=![]() ×2×5﹣
×2×5﹣![]()
=5﹣π.
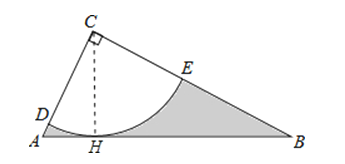
【解析】(1)过点C作CH⊥AB于H,如图,先在Rt△ABC中,利用正切的定义计算出BC=2AC=2![]() ,再利用勾股定理计算出AB=5,接着利用面积法计算出CH=2,则可判断CH为⊙C的半径,然后根据切线的判定定理即可得到AB为⊙C的切线;
,再利用勾股定理计算出AB=5,接着利用面积法计算出CH=2,则可判断CH为⊙C的半径,然后根据切线的判定定理即可得到AB为⊙C的切线;
(2)根据三角形面积公式和扇形的面积公式,利用S阴影部分=S△ACB﹣S扇形CDE进行计算即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A.经过直线外一点,有且仅有一条直线与一线与已知直线垂直
B.平分弦的直径垂直于弦
C.对角线互相平分且垂直的四边形是菱形
D.反比例函数y= ![]() ,当k<0时,y随x的增大而增大
,当k<0时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P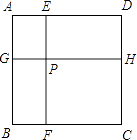
(1)若AG=AE,证明:AF=AH;
(2)若矩形PFCH的面积,恰矩形AGPE面积的两倍,试确定∠HAF的大小;
(3)若矩形EPHD的面积为 ![]() ,求Rt△GBF的周长.
,求Rt△GBF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一些体积为1![]() 的小立方体恰好可以组成体积为1
的小立方体恰好可以组成体积为1![]() 的大立方体,把所有这些小立方体一个接一个向上摞起来,大概有多高呢?以下选项中最接近这一高度的是( )
的大立方体,把所有这些小立方体一个接一个向上摞起来,大概有多高呢?以下选项中最接近这一高度的是( )
A. 莲花山望海观音的高度 B. 滴水岩森林公园青萝嶂高度
C. 广州塔的高度 D. 国际航班飞行高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在
在![]() 的内部,OM平分
的内部,OM平分![]() ,ON平分
,ON平分![]()
(1)如图1,![]() 时,当OC在OD的左侧,求
时,当OC在OD的左侧,求![]() 的度数.
的度数.
(2)如图2,![]() 时,当OC在OD的右侧 ,请补全图形,并求
时,当OC在OD的右侧 ,请补全图形,并求![]() 的度数.
的度数.
(3)如图3,当![]() ,且OC在OD左侧时,试用
,且OC在OD左侧时,试用![]() 的代数式表示
的代数式表示![]() .
.
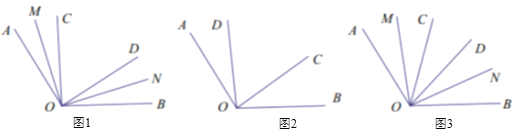
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市准备将一批帐篷和食品送往扶贫区.已知帐篷和食品共320件,且帐篷比食品多80件.
(1)直接写出帐篷有 件,食品有 件;
(2)现计划租用A、B两种货车共8辆,一次性将这批物资全部送到扶贫区,已知两种车可装帐篷和食品的件数以及每辆货车所需付运费情况如表,问:共有几种租车的方案?最少运费是多少?
帐篷(件) | 食品(件) | 每辆需付运费(元) | |
A种货车 | 40 | 10 | 780 |
B种货车 | 20 | 20 | 700 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴相交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).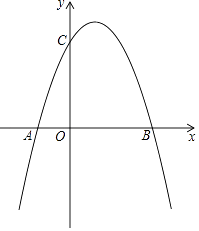
(1)求抛物线的解析式;
(2)连接BC,点P为抛物线上第一象限内一动点,当△BCP面积最大时,求点P的坐标;
(3)设点D是抛物线的对称轴上的一点,在抛物线上是否存在点Q,使以点B,C,D,Q为顶点的四边形为平行四边形?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com