
【题目】某市准备将一批帐篷和食品送往扶贫区.已知帐篷和食品共320件,且帐篷比食品多80件.
(1)直接写出帐篷有 件,食品有 件;
(2)现计划租用A、B两种货车共8辆,一次性将这批物资全部送到扶贫区,已知两种车可装帐篷和食品的件数以及每辆货车所需付运费情况如表,问:共有几种租车的方案?最少运费是多少?
帐篷(件) | 食品(件) | 每辆需付运费(元) | |
A种货车 | 40 | 10 | 780 |
B种货车 | 20 | 20 | 700 |
【答案】(1)200,120;(2)方案见解析,最少运费是5760元
【解析】
(1)有两个等量关系:帐篷件数+食品件数=320,帐篷件数-食品件数=80,直接设未知数,列出一元一次方程,求出解;
(2)先由等量关系得到一元一次不等式组,求出解集,再根据实际含义确定方案;分别计算每种方案的运费,然后比较得出结果.
(1)设食品x件,则帐篷(x+80)件,由题意,得
x+(x+80)=320,
解得:x=120.
则帐篷有120+80=200件.
故答案为200,120;
(2)设租用A种货车a辆,则B种货车(8﹣a)辆,由题意,得
![]() ,
,
解得:2≤a≤4.
∵a为整数,
∴a=2,3,4.
∴B种货车为:6,5,4.
∴租车方案有3种:
方案一:A车2辆,B车6辆;
方案二:A车3辆,B车5辆;
方案三:A车4辆,B车4辆;
3种方案的运费分别为:
①2×780+6×700=5760(元);
②3×780+5×700=5840(元);
③4×780+4×700=5920(元).
则方案①运费最少,最少运费是5760元.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3)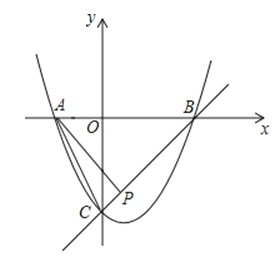
(1)求抛物线的函数表达式.
(2)求直线BC的函数表达式和∠ABC的度数.
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() ,半径为2的⊙C,分别交AC,BC于点D,E,得到
,半径为2的⊙C,分别交AC,BC于点D,E,得到![]() .
. 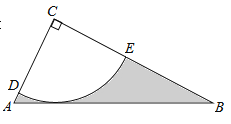
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( ) 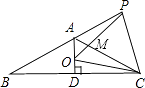
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力 | 科研能力 | 组织能力 | |
甲 | 81 | 85 | 86 |
乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
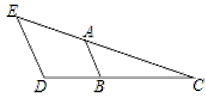
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com